こんにちは。以下個人的な感想です。第3回の基礎学力テスト拝見しました。今回の数学のテストの内容は昨年の高校入試を模してますね?それは, 情報量は多いけど, 問題の難易度はそんなに高くないという問題構成から読み取れます。恐らく今年の高校入試の一般選抜試験もそうなるだろうと予想して, 今回基礎学の問題を作成されたのだと思います。この大問5だけ違う世界にいるような問題だったので, 今回これを解説します。
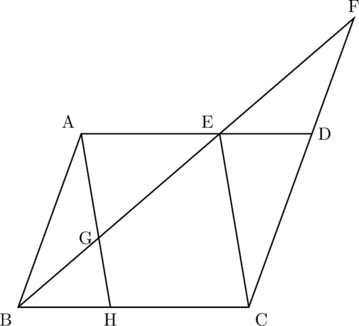
【問題】下の図の四角形ABCDは平行四辺形である。点Eは辺AD上の点であり, 直線BEと直線CDの交点を点Fとする。点E, Cを結び, 点Aから線分ECに平行な直線をひき, その直線と直線BF, 辺BCとの交点をそれぞれ点G, Hとする。次の(1)・(2)に答えなさい。
(1) ![]() ∽
∽![]() であることを証明しなさい。
であることを証明しなさい。
(2) ![]() のとき, 次の
のとき, 次の![]() に答えなさい。
に答えなさい。![]()
![]() の面積と
の面積と![]() の面積の比を最も簡単な整数の比で表しなさい。
の面積の比を最も簡単な整数の比で表しなさい。![]()
![]() のとき, GEの長さを求めなさい。
のとき, GEの長さを求めなさい。
【解答・解説】
(1) ![]() と
と![]() において,
において,
仮定より, ![]() より錯角は等しいので,
より錯角は等しいので, ![]()
対頂角は等しいので, ![]()
![]() より同位角は等しいので,
より同位角は等しいので, ![]()
![]() より,
より, ![]()
![]() より2組の角がそれぞれ等しいので,
より2組の角がそれぞれ等しいので, ![]() ∽
∽![]()
【別解(略解)】同じようなやり方で, 半直線CE上に点Pを辺ADより上側にとって, 同位角が等しい, そして対頂角が等しいという流れでも証明できる。さらに, 四角形ABCDと四角形AHCEが平行四辺形であることから証明する方法もある。
(2) ![]() 各辺の比を書くと以下のようになる。同じ色が対応している。
各辺の比を書くと以下のようになる。同じ色が対応している。
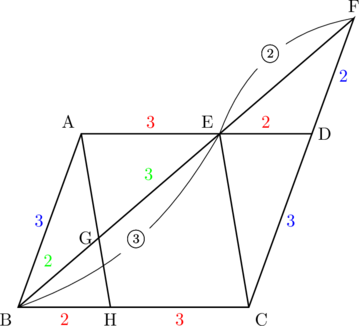
よって,
よって, 面積比は
【別解(略解)】面積の割合を決めてから解く方法もありますが, 煩雑になるのでお勧めはしません。
四角形AHCEは平行四辺形(2組の辺がそれぞれ平行)である。したがって,
ここで,
【別解(略解)】連比(比合わせ)を用いる方法もありますが, 今回はそれを使わなくても大丈夫な例です。
 数樂管理人のブログ
数樂管理人のブログ 


