中学数学：攻略法：平行線と角の問題の見るべきポイント

こんにちは。平行線と角ではどこを見るべきか書いておきますね。それではどうぞ。

平行線と角の問題はこう見る

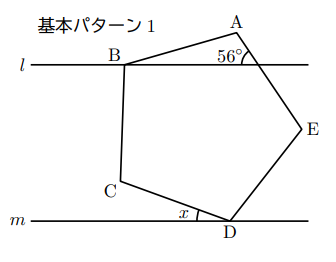
下の図1のように, 正五角形ABCDEの頂点B, Dを通る直線をそれぞれとする。であるとき,　の大きさを求めなさい。

よく聞かれる問題であるが, この手の問題平行線の中でくの字に折れ曲がっている問題(平行線にくの問題と呼んでいる)の攻略方法は, くの字のとんがっているところに平行線を引くと, ほとんどの場合で解決が可能。
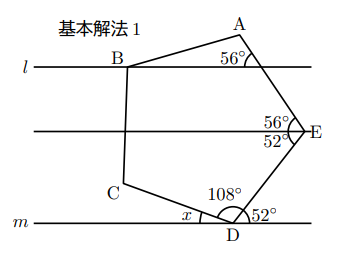
この問題ではEからに平行な直線を引くと, 同位角, 錯角ができ, その角の大きさは基本解法1のようである。
したがって,

となる。別にくの字に折れ曲がっている箇所が複数あっても同じで, この解法で答えは出せます。
この解法を1つ知っておけば, この手の問題には対応できるというだけで, 場合によっては他の解法が有効な場合もあると考える。

では, 次にいってみたい。
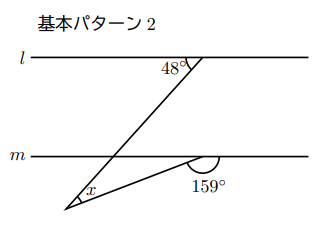
下の図2において, 2直線, は平行である。このとき, の大きさを求めなさい。

この問題では, 平行線の中にくの字はなく, 平行線の外側に三角形がはみ出している図になっている。
この手の問題は, このはみ出した三角形を用いて答えを得るのがほとんどである。
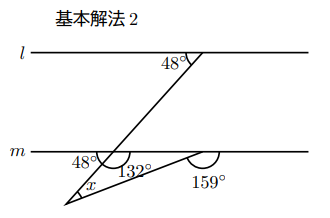
同位角の関係などにより, 基本解法2のような角の大きさとなり, 平行線の外側にできた三角形において, 内角と外角の関係から,

となる。

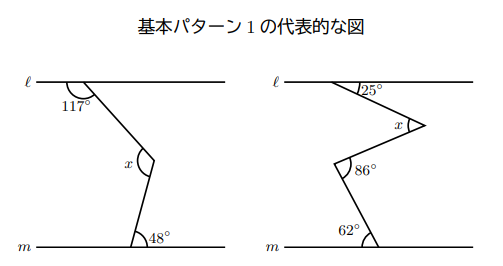
次に基本パターン1の代表的な図を2つ書いておく。ご参考にしてください。

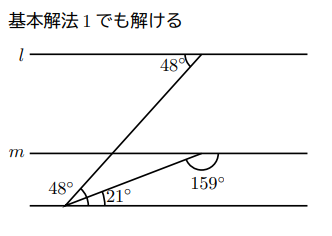
前に基本解法2を紹介したが, あの問題も実は基本解法1で解くことができる。解法を基本解法1に1本化してもよいが, 少々ナンセンス？かなと思って基本解法2を紹介してある。解法に関しては個人の自由だと思っているので, これらはあくまで参考にしていただきたい。
基本解法1で解くと

となる。

プリントアウト用pdf