中学数学：攻略法：正多角形が絡む角度の問題の見るべきポイント

こんにちは。角度の問題の攻略法というか気づくべきポイントを書いておきます。

気づくべきポイント

多角形で対角線を引いた角の問題や多角形の組み合わせの角の問題では, 二等辺三角形を見つけて,その角を調べていけば片付く問題がほとんどである。
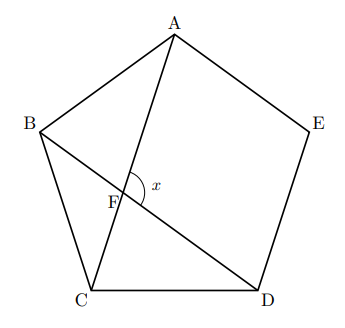
例えば図1の正五角形の問題では, $\text{AB=BC}$ , $\text{BC=CD}$ なので, $\bigtriangleup{\text{ABC}}$ , $\bigtriangleup{\text{CDB}}$ が頂角108 $\Deg$ の二等辺三角形であることがわかる。だから2つの底角は, $72\div2=36\Deg$ となる。後はその図形が重なっているだけなので, 調べていけば解ける。図1の答えは $\angle{x}=108\Deg$ である。

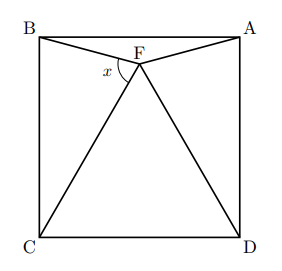
続いての図2は, 正三角形FCDと正方形ABCDの組み合わせである。この場合も同じで二等辺三角形を探す。
この場合, 慣れていないと俊敏には発見できないかもしれないが, $\text{CB=CF}$ , $\text{DF=DA}$ より, $\bigtriangleup{\text{CFB}}$ , $\bigtriangleup{\text{DAF}}$ が二等辺三角形であることがわかる。また, $\bigtriangleup{\text{AFB}}$ も二等辺三角形である。ただ, 頂角がすぐにわかるのは $\bigtriangleup{\text{CFB}}$ , $\bigtriangleup{\text{DAF}}$ の2つである。ちなみにこの2つの三角形は合同。合同であるから $\text{FB=FA}$ となり, $\bigtriangleup{\text{AFB}}$ は二等辺三角形となる。話は少しそれましたが, この $\bigtriangleup{\text{CFB}}$ , $\bigtriangleup{\text{DAF}}$ の頂角は正方形の1つの角(90 $\Deg$ )から正三角形の1つの角(60 $\Deg$ )を引いた30 $\Deg$ が頂角になる。よって求める $\angle{x}$ は $(180\Deg-30\Deg)\div2=75\Deg$ となる。