こんにちは。代表的な問題には解法がある。その典型です。それではどうぞ。
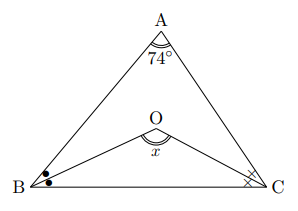
下の図1で, ![]() の
の![]() ,
, ![]() の二等分線の交点(内心)のなす角
の二等分線の交点(内心)のなす角![]() を求めなさい。
を求めなさい。
まずは, 学校で習うだろう解法で解いてみましょう。![]()
だから, ![]()
よって, ![]()
![]()
生徒:難しい![]() もっと簡単な方法ないの?
もっと簡単な方法ないの?
実は公式があってね![]()
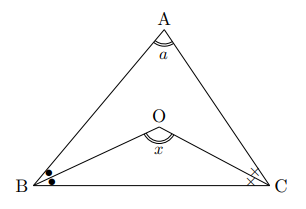
下の図2のように![]() 場合,
場合, ![]() は次の公式で求められるんです。
は次の公式で求められるんです。![]()
これを使うと, ![]()
ほら, 同じ答えになった。公式の証明は後述します。
でも, 実は僕この公式使ったことないんです。公式が覚えられる人は覚えてください。覚えられる人は解法を覚えておくと他の人より, 少し早く答えにたどり着きます。
中学校で必要な公式はそんなに多くはありません。これは無理して覚えなくてもいいです。
では公式が覚えられないための人へのリーサルウェポン(最終兵器)です。これで駄目でもこれ以外, 解き方解き方知りません。
では行きましょう。今わかっている角は![]() 残りの角の和は
残りの角の和は![]() です。
です。
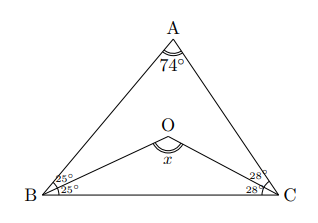
これ(![]() )を0以外の2つの偶数に分けてください。別に偶数でなくてもいいですが, 途中で小数が出てくる羽目になるので, できれば偶数にしてください。決まりましたか?
)を0以外の2つの偶数に分けてください。別に偶数でなくてもいいですが, 途中で小数が出てくる羽目になるので, できれば偶数にしてください。決まりましたか?![]() と
と![]() です。OBとOCは角の二等分線なので, その半分ずつ
です。OBとOCは角の二等分線なので, その半分ずつ![]() と
と![]() に分けることができますね。
に分けることができますね。![]() で2つの内角が
で2つの内角が![]() と
と![]() になっていますね。ですから求める
になっていますね。ですから求める![]() は
は![]()
別に![]() と
と![]() でも大丈夫です。半分は
でも大丈夫です。半分は![]() と
と![]() ですから,
ですから, ![]() 同じです。
同じです。
前のところで![]() が分かっていて,
が分かっていて, ![]() を求める場合でも使えます。
を求める場合でも使えます。
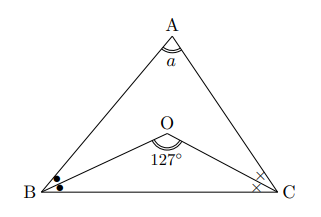
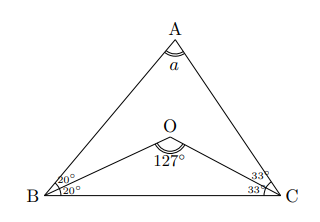
この場合は別に偶数に分けなくても2倍しますので大丈夫です。右の図のように127![]() の場合, 残りの角は
の場合, 残りの角は![]() 。図のように
。図のように![]() 、
、![]() に分けると, それぞれその2倍が
に分けると, それぞれその2倍が![]() ,
, ![]() の大きさなので,
の大きさなので, ![]() ,
, ![]() となる。
となる。
よって, ![]()
ちなみに, ![]() を求める公式
を求める公式![]()
【補足】公式の証明
【証明】![]()
![]() より,
より, ![]()
ここで, ![]() で,
で, ![]()
![]() を代入して,
を代入して, 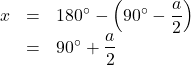
よって, ![]()
![]() を
を![]() について解くと,
について解くと, ![]()
 数樂管理人のブログ
数樂管理人のブログ