中学数学：相似：初めて相似を学ぶ方へ

こんにちは。初めて相似を学ぶ方向けに書きました。それではどうぞ。

相似な関係

まず相似とは何かというと, ある図形を一定の割合で拡大, または縮小した図形ともとの図形の関係のことを言います。拡大とは, 形を変えずに大きくすることで, 縮小とは形を変えずに小さくすることを言います。
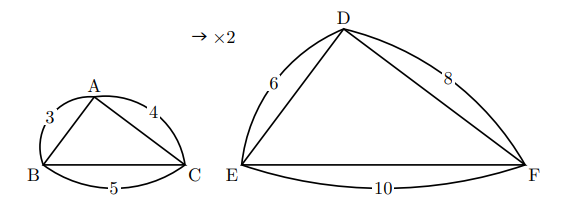
下の図のような $\bigtriangleup{\text{ABC}}$ と $\bigtriangleup{\text{DEF}}$ は相似な関係にあるといいます。
なぜなら, $\bigtriangleup{\text{DEF}}$ は $\bigtriangleup{\text{ABC}}$ の2倍の拡大図になっているからです。

このとき, 対応する辺(線分)の比はみな等しくなっています。
$\text{AB : DE= 3 : 6=1 : 2}$
$\text{BC : EF= 5 : 10=1 : 2}$
$\text{CA : FD= 4 : 8=1 : 2}$
この対応する辺の比(ここでは $1 : 2$ )のことを相似比といいます。このように,相似比は対応する辺において一定です。また, 形は変わっていないわけですから, 対応する角の大きさはみな等しくなっています。
$\kaku{A}=\kaku{D}$
$\kaku{B}=\kaku{E}$
$\kaku{C}=\kaku{F}$
ここまでをまとめると,

相似な図形の性質

$\maru1$ 対応する辺(線分)の比はすべて等しい
$\maru2$ 対応する角の大きさはそれぞれ等しい

そして上の相似な図形の関係を, 合同と同じように記号∽(読み方は相似)を使って表すと,
$\bigtriangleup{\text{ABC}}$ ∽ $\bigtriangleup{\text{DEF}}$
と表すことができます。
書き方は合同な図形の表し方と同じで, 対応する頂点をそろえて書きます。
最後に余談ではありますが, 相似比が1 : 1の場合の図形の関係は, 合同な関係になります。
お粗末でした。勉強の参考にしてください。

相似な関係

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル