こんにちは。面積比は相似比の2乗に比例するという話です。それではどうぞ。
下の図のような![]() と
と![]() があります。相似比は
があります。相似比は![]() である。このとき, 面積比が
である。このとき, 面積比が![]() となることを証明してみましょう。
となることを証明してみましょう。
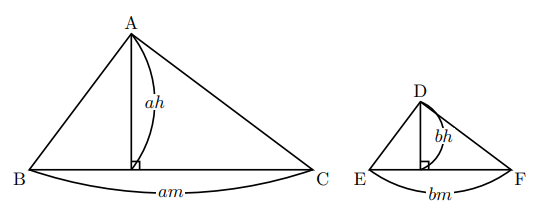
以下三角形限定で証明させていただきます。![]() を自然数,
を自然数, ![]() を正の数とし相似比が
を正の数とし相似比が![]() の三角形の底辺である辺BC, EFをそれぞれ,
の三角形の底辺である辺BC, EFをそれぞれ, ![]() ,
, ![]() , 頂点A, Dから底辺におろした高さを
, 頂点A, Dから底辺におろした高さを![]() ,
, ![]() とおく。(注:相似比が
とおく。(注:相似比が![]() ということは高さの関係も相似なのでその比は
ということは高さの関係も相似なのでその比は![]() とおける)ここで
とおける)ここで![]() ,
, ![]() の面積をそれぞれ
の面積をそれぞれ![]() とおくと,
とおくと,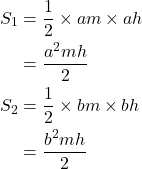
よって面積比![]() は
は![]()
従って, 相似比が![]() の三角形の面積比は
の三角形の面積比は![]() である。三角形なら, 直角二等辺三角形が証明としてはやりやすい。また正方形や円を証明に用いれば, もっとすっきりする。他の多角形の場合はおそらく,三角形の組み合わせで証明できるんじゃないの?ということで今回三角形に特化して証明しました。
である。三角形なら, 直角二等辺三角形が証明としてはやりやすい。また正方形や円を証明に用いれば, もっとすっきりする。他の多角形の場合はおそらく,三角形の組み合わせで証明できるんじゃないの?ということで今回三角形に特化して証明しました。
ただ, 感覚的に面積の単位cm![]() からわかるように, 辺を2回かけることがわかります。すなわち, 相似比が
からわかるように, 辺を2回かけることがわかります。すなわち, 相似比が![]() なら,
なら, ![]() という割合の辺を2回かける,
という割合の辺を2回かける, ![]() という割合の辺を2回かけることから, 面積比は
という割合の辺を2回かけることから, 面積比は![]() と考えてもいいでしょう。
と考えてもいいでしょう。
 数樂管理人のブログ
数樂管理人のブログ