こんにちは。体積比は相似比の3乗になることを簡単に触れておきます。それではどうぞ。
相似比が![]() の立体で, その体積比が
の立体で, その体積比が![]() になるのはなぜか見てみたいと思います。以下に相似比が
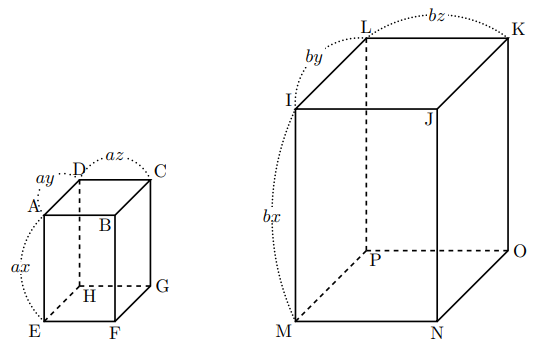
になるのはなぜか見てみたいと思います。以下に相似比が![]() の直方体があります。各辺の長さを図のように置くとき,
の直方体があります。各辺の長さを図のように置くとき,
上図の左側の体積![]() は
は![]()
右側の体積![]() は
は![]()
よって, 2つの体積比は![]()
となる。実際に手短に説明するときは立方体をモデルとした方が理解しやすいかと考える。球も考えやすいと思うが, 公式自体を忘れていることが多いので, 手短になら立方体かなと思う。その他の図形で証明するときは, 自分で設定してみるのも面白い。
ただ, 感覚的に面積の単位cm![]() からわかるように, 辺を3回かけることがわかります。すなわち, 相似比が
からわかるように, 辺を3回かけることがわかります。すなわち, 相似比が![]() なら,
なら, ![]() という割合の辺を3回かける,
という割合の辺を3回かける, ![]() という割合の辺を3回かけることから, 面積比は
という割合の辺を3回かけることから, 面積比は![]() と考えてもいいでしょう。
と考えてもいいでしょう。
 数樂管理人のブログ
数樂管理人のブログ