中学数学：R6(2024)年度徳島県公立高校入試・数学・規則性

こんにちは。図をつくるの大変だから, 入試問題スキャンして図を引用しました。不適切だったら削除するのでよろしくお願いします。

規則性

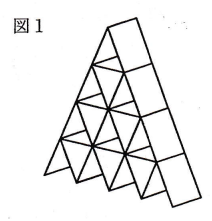
まことさんは, トランプを使って図1のようなタワーをつくろうと考えた。できるだけ大きなタワーをつくるために, 必要なトランプの枚数を調べることにした。(1)・(2)に答えなさい。

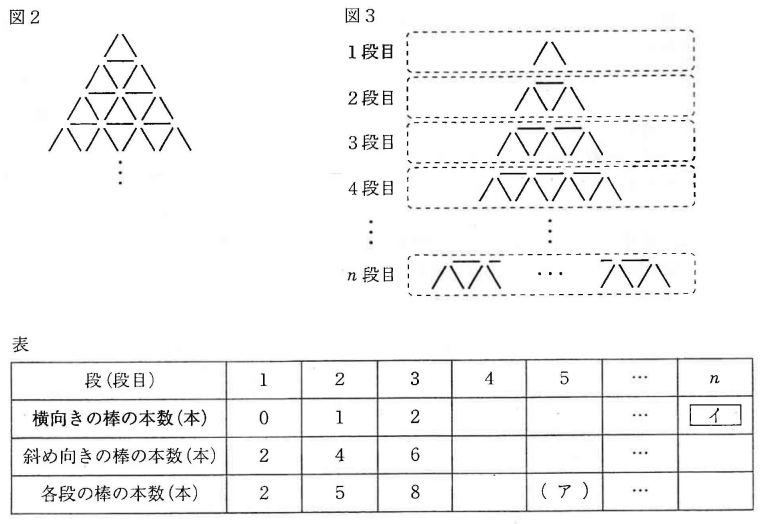
(1) まことさんは, 図2のように, トランプの代わりに同じ長さの棒を並べたモデルをつくり, 棒の本数を数えることでトランプの枚数を調べることにした。(a)・(b)に答えなさい。
(a) まことさんは, 図3のように, 上から1段目, 2段目, 3段目, 4段目, $\cdots$ , $n$ 段目と分けて, 各段の棒の本数を, 横向きの棒と斜め向きの棒に着目して, 下のような表にまとめようとしている。表の(ア)にあてはまる数を, イにあてはまる $n$ を用いた式を, それぞれ書きなさい。

(b) トランプ1組54枚を使うと最大何段のタワーをつくることができるか, 求めなさい。ただし, 使わないトランプがあってもよいものとする。
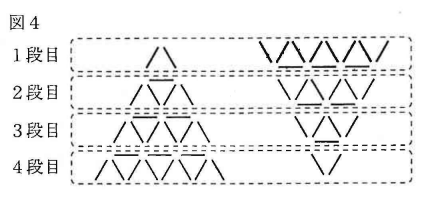
(2) まことさんは, タワーをつくるために, 必要なトランプの枚数を効率的に調べる方法について, 次のように考えをまとめた。(a)・(b)に答えなさい。
【まことさんの考え】
[4段のとき]
図4のように, 4段のモデルと, 同じものを逆さまにしたモデルを組み合わせて, 上から1段目, 2段目, 3段目, 4段目を考えると, 各段の棒の本数は, それぞれ(ウ)本で同じになる。

このことを利用すれば, 4段のタワーに必要なトランプの枚数を求めることができる。
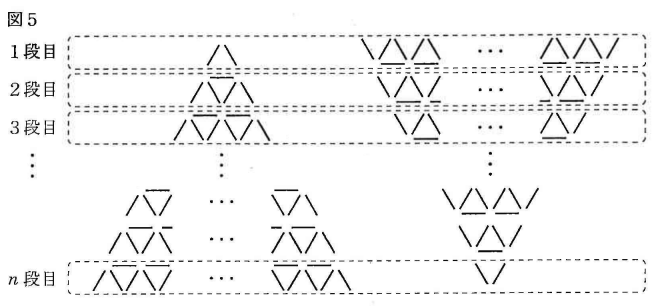
[ $n$ 段のとき]
図5のように, $n$ 段のモデルと, 同じものを逆さまにしたモデルを組み合わせて, 上から1段目, 2段目, 3段目, $\cdots$ , $n$ 段目を考えると, 各段の棒の本数は, それぞれ(エ)本で同じになる。

これらの考え方を利用すれば, 何段のタワーであっても, 必要なトランプの枚数を求めることができる。
(a) 【まことさんの考え】の(ウ)にあてはまる数を, エにあてはまる $n$ を用いた式を, それぞれ書きなさい。
(b) 20段のタワーをつくるために, 必要なトランプは何枚か, 求めなさい。

解答・解説

(1) (a)各段の本数は3本ずつ増えているので, 5番目は14本
ア $14\cdots$ (答)
1段目0, 2段目1, 3段目2, $\cdots$ , $n$ 段目 $n-1$
イ $n-1\cdots$ (答)
(1) (b)各段の棒の本数を小さい順に足していくと,
$2+5+8+11+14=40$ , $2+5+8+11+14+17=57$
よって, 14のときまでしかトランプは使えない。
したがって, 5段目 $\cdots$ (答)
(2) (a)各段の和は13になっている。
ウ $13\cdots$ (答)
$n$ 段目の枚数は $3n-1$ (本)なので, 各段の合計は $2+3n-1=3n+1$
エ $3n+1\cdots$ (答)
(b) 逆さまにして合わせたときの各段の合計は $3\times20+1=61$ , それが20段あるので, $61\times20=1220$ 。同じものを2つたしているので, $1220\div2=610$
$610$ 枚 $\cdots$ (答)

規則性

解答・解説

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル