こんにちは。有名問題からどうぞ。
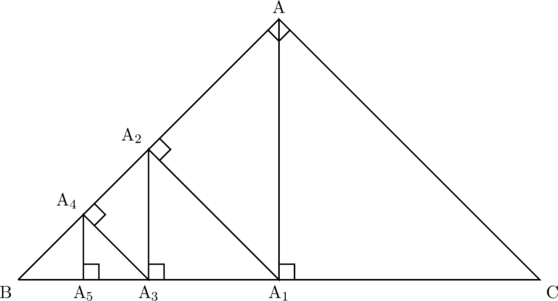
直角二等辺三角形の頂点AからBCに垂線![]() を下ろす。
を下ろす。![]() からABに垂線
からABに垂線![]() を下ろし, 以下図のように続けていくとき,
を下ろし, 以下図のように続けていくとき, ![]() を求めよ。ただし,
を求めよ。ただし, ![]() とする。
とする。
【日本女子大】
【解答】![]()
【解説】![]() ,
, ![]() ,
, ![]() ,
, ![]()
漸化式をつくると, ![]() , ただし,
, ただし, ![]() とする。
とする。
よって, 一般項は, 初項![]() , 公比
, 公比![]() の等比数列。
の等比数列。
つまり, ![]()
したがって, この無限級数和は, 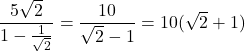
こんにちは。有名問題からどうぞ。
直角二等辺三角形の頂点AからBCに垂線![]() を下ろす。
を下ろす。![]() からABに垂線
からABに垂線![]() を下ろし, 以下図のように続けていくとき,
を下ろし, 以下図のように続けていくとき, ![]() を求めよ。ただし,
を求めよ。ただし, ![]() とする。
とする。

【日本女子大】
【解答】![]()
【解説】![]() ,
, ![]() ,
, ![]() ,
, ![]()
漸化式をつくると, ![]() , ただし,
, ただし, ![]() とする。
とする。
よって, 一般項は, 初項![]() , 公比
, 公比![]() の等比数列。
の等比数列。
つまり, ![]()
したがって, この無限級数和は,