こんにちは。結構有名な原理なので知らない人は知っておきましょう。
連立方程式を解いていて, 余計な答えが求まった。そんな経験はありませんか?
例えば以下の連立方程式を解いてみましょう。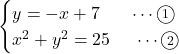
これを解くときに, ![]() を
を![]() に代入して,
に代入して, ![]()
![]() となり,
となり, ![]() を得る。
を得る。
ここまでは, いつも通りなんですが,
この![]() の値を
の値を![]() に代入するのか,
に代入するのか, ![]() に代入するのかで, 答えが変わってくるんですよね。
に代入するのかで, 答えが変わってくるんですよね。![]() に代入した場合,
に代入した場合, ![]() を
を![]() に代入すると,
に代入すると, ![]()
![]() を
を![]() に代入すると,
に代入すると, ![]()
よって, 求める解は, ![]() の2解となる。
の2解となる。![]()
次に![]() に代入した場合,
に代入した場合, ![]() を
を![]() に代入すると,
に代入すると, ![]() となり,
となり, ![]() ,
, ![]() を
を![]() に代入すると,
に代入すると, ![]() となり,
となり, ![]()
となる。
よって, 求める解は, ![]() の4解となる。
の4解となる。![]()
???
どちらが正しいの?ってなりますが, 冷静に考えてみると,![]() が正しいですね。
が正しいですね。![]() の解には
の解には![]() を満たさないものまで含まれています。
を満たさないものまで含まれています。
これをきちんと理解していくのが代入性の原理というものです。
同値性を意識して式を見ていきましょう。解![]() が求められる場合,
が求められる場合, 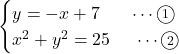
![]() を
を![]() に代入した場合,
に代入した場合, 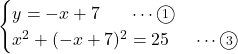
となり, これからこの![]() ,
, ![]() の組み合わせから,
の組み合わせから, ![]() ,
, ![]() の式は作れますし, 逆もまたいえることができます。すなわち同値性が保たれていることになります。
の式は作れますし, 逆もまたいえることができます。すなわち同値性が保たれていることになります。
しかし, 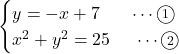
![]() を
を![]() に代入し,
に代入し, 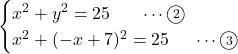
とした場合, これからこの![]() ,
, ![]() の組み合わせから,
の組み合わせから, ![]() ,
, ![]() の式は作れますが,
の式は作れますが, ![]() ,
, ![]() からは,
からは, ![]() ,
, ![]() を再現できません。すなわち同値性は保たれていないことになります。
を再現できません。すなわち同値性は保たれていないことになります。![]() ,
, ![]() は
は![]() ,
, ![]() であるための必要条件になっている。
であるための必要条件になっている。
このことから, ![]() ,
, ![]() で解いた答えには, 余計なものが含まれている可能性があるため,
で解いた答えには, 余計なものが含まれている可能性があるため, ![]() に代入して十分性を確認する必要があります。
に代入して十分性を確認する必要があります。
代入性の原理
代入した元の式と, 代入した式が残ることで, 同値性を確保することができる。
これが代入性の原理の正体であります。
 数樂管理人のブログ
数樂管理人のブログ 

