こんにちは。定番のいい問題ですよ。それではどうぞ。
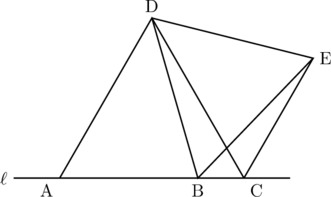
下の図のように, 直線![]() 上に3点A, B, Cをとり, 辺ACを一辺とする正三角形ACDと辺DBを一辺とする正三角形BEDをつくり, 点Cと点Eを結ぶ。このとき, 次の(1)・(2)の問いに答えなさい。
上に3点A, B, Cをとり, 辺ACを一辺とする正三角形ACDと辺DBを一辺とする正三角形BEDをつくり, 点Cと点Eを結ぶ。このとき, 次の(1)・(2)の問いに答えなさい。
(1) ![]() を証明しなさい。
を証明しなさい。
(2) ![]() のとき, 四角形BCEDの面積を求めなさい。
のとき, 四角形BCEDの面積を求めなさい。
【解答】
(1) ![]() と
と![]() において,
において, ![]() と
と![]() は正三角形なので,
は正三角形なので, ![]()
![]()
また, ![]()
![]()
より, ![]()
![]() より,
より,
2組の辺とその間の角がそれぞれ等しいので, ![]()
(2)
四角形BCED![]()
よって, 求める面積は一辺が4cmの正三角形の面積と等しい。
したがって, ![]()
![]() (答)
(答)
 数樂管理人のブログ
数樂管理人のブログ 


