こんにちは。今回は置換積分法について書いておきます。以下![]() は積分定数とします。
は積分定数とします。
【考え方】![]() とおくと,
とおくと, ![]()
【証明】![]() を微分して,
を微分して, ![]()
したがって, ![]()
同様に![]() なら,
なら, ![]()
【証明】![]() とおくと,
とおくと,![]() なので,
なので, ![]()
したがって, 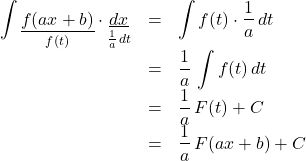
1次式の累乗式の積分(2乗程度なら展開してもよいが![]() )
)![]()
![]() なら,
なら, ![]()
![]() なら,
なら, ![]()
また, ![]() は
は![]() として積分し,
として積分し, ![]() は
は![]() として積分するとよい。
として積分するとよい。
【例1】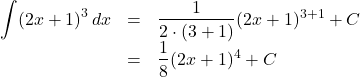
【例2】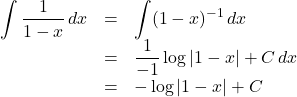
【例3】![Rendered by QuickLaTeX.com \begin{array}{lll}\displaystyle\int \dfrac{1}{\sqrt[4]{(1-x)^3}}\,dx&=&\displaystyle\int(1-x)^{-\frac34}\,dx\\&=&\dfrac{1}{\left(-\frac34+1\right)\cdot(-1)}(1-x)^{\left(-\frac34+1\right)}+C\\&=&-4(1-x)^{\frac14}+C\\&=&-4\sqrt[4]{1-x}+C\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-7f12f493755faefe4ccd0b053877476e_l3.png)
![]() と
と![]() が積の形の積分
が積の形の積分![]()
【例1】![]()
![]() とおくと,
とおくと, ![]() なので,
なので, ![]()
よって, 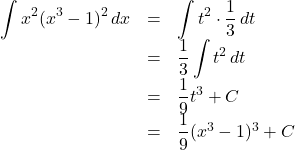
公式を使った例
【例2】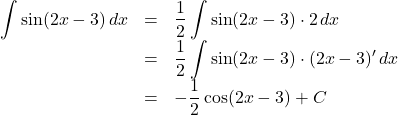
![]() が分子で
が分子で![]() が分母になっている形の積分
が分母になっている形の積分![]()
【例1】![]()
![]() とおくと,
とおくと, ![]() なので,
なので, ![]()
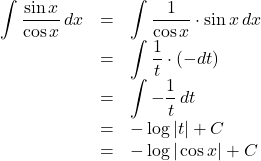
公式で解決すると, 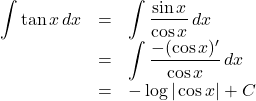
【例2】公式利用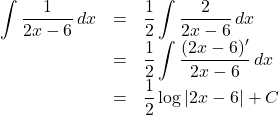
 数樂管理人のブログ
数樂管理人のブログ 

