高校数学：数III微分・無理式の分数関数の微分

こんにちは。今回は無理関数の微分で, 分数になっている場合をやってみようと思います。それではみていきましょう。

分数の無理関数の微分のコツ

$\left\{\dfrac{f(x)}{g(x)}\right\}$ で, $f(x)$ や $g(x)$ が無理式のときは, $\left\{f(x)\cdot g(x)^{-1}\right\}$ として, 積の微分法を用いるとよい。

【例】関数 $y=\sqrt[3]{\dfrac{x-1}{x}}$ を微分せよ。

【解答例】
$y=\sqrt[3]{x-1}\cdot\sqrt[3]{x}^{-1}=(x-1)^{\frac13}\cdot x^{-\frac13}$ なので,
$\begin{array}{lll}y'&=&\dfrac13(x-1)^{\frac13-1}\cdot x^{-\frac13}\cdot (x-1)'-\dfrac13\cdot (x-1)^{\frac13}\cdot x^{-\frac13-1}\\&=&\dfrac13(x-1)^{-\frac23}\cdot x^{-\frac13}-\dfrac13(x-1)^{\frac13}\cdot x^{-\frac43}\\&=&\dfrac{1}{3\sqrt[3]{x}\sqrt[3]{(x-1)^2}}-\dfrac{\sqrt[3]{x-1}}{3x\sqrt[3]{x}}\\&=&\dfrac{x-(x-1)}{3x\sqrt[3]{x}\sqrt[3]{(x-1)^2}}\\&=&\dfrac{1}{3x\sqrt[3]{x}\sqrt[3]{(x-1)^2}}\end{array}$
もちろんこれ以外に以下の解法もある。
【解答例】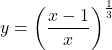
$y=\left(\dfrac{x-1}{x}\right)^{\frac13}$ として微分すると,
$\begin{array}{lll}y'&=&\dfrac13\left(\dfrac{x-1}{x}\right)^{\frac13-1}\cdot\left(\dfrac{x-1}{x}\right)'\\&=&\dfrac13\left(\dfrac{x-1}{x}\right)^{-\frac23}\cdot\dfrac{1}{x^2}\\&=&\dfrac{1}{3\sqrt[3]{\dfrac{(x-1)^2}{x^2}}}\cdot\dfrac{1}{\sqrt[3]{x^6}}\\&=&\dfrac{1}{3\sqrt[3]{x^4}\sqrt[3]{(x-1)^2}}\\&=&\dfrac{1}{3x\sqrt[3]{x}\sqrt[3]{(x-1)^2}}\end{array}$

分母の有理化

分数式の無理関数の微分では, 分母の有理化を行うとスムースにできることもある。

【例】関数 $y=\dfrac{1}{\sqrt{x}-\sqrt{x+1}}$ を微分せよ。

【解答例】
関数の右辺の分母の有理化を行うと,
$\dfrac{\sqrt{x}+\sqrt{x+1}}{(\sqrt{x}-\sqrt{x+1})(\sqrt{x}+\sqrt{x+1})}=-\sqrt{x}-\sqrt{x+1}$
よって, 与式の関数は,
$y=-\sqrt{x}-\sqrt{x+1}$ となり, $y=-x^{\frac12}-(x+1)^{\frac12}$ となるので,
$\begin{array}{lll}y'&=&-\dfrac12x^{-\frac12}-\dfrac12(x+1)^{-\frac12}\cdot(x+1)'\\&=&-\dfrac{1}{2\sqrt{x}}-\dfrac{1}{2\sqrt{x+1}}\\&=&-\dfrac{\sqrt{x+1}+\sqrt{x}}{2\sqrt{x(x+1)}}\end{array}$

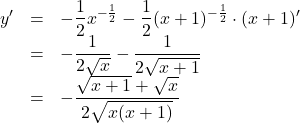
無理式の分数関数の微分

$\left\{\dfrac{f(x)}{g(x)}\right\}$ で, $f(x)$ や $g(x)$ が無理式のときは, $\left\{f(x)\cdot g(x)^{-1}\right\}$ として, 積の微分法を用いるとよい。また, 分母の有理化を行うことでスムースに微分が行える場合がある。

分数の無理関数の微分のコツ

分母の有理化

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル