こんにちは。今回は逆関数の微分法について書いておきます。
関数![]() の逆関数を
の逆関数を![]() とすると,
とすると, ![]() となります。
となります。![]() を
を![]() で微分すると,
で微分すると, ![]()
となります。
したがって,![]()
また, ![]() を
を![]() で微分すると,
で微分すると, ![]() となるので, これを
となるので, これを![]() にあてはめると,
にあてはめると, 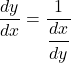
となります。
逆関数の微分を使う場面は, ![]() 逆関数をとった方が楽な場合, つまり,
逆関数をとった方が楽な場合, つまり, ![]() を
を![]() とした方がよい場合。
とした方がよい場合。![]()
![]() の形で表せない場合に用いるとよい。
の形で表せない場合に用いるとよい。
以下に![]() の例題を示しました。
の例題を示しました。
【![]() の例】関数
の例】関数![]() を微分せよ。
を微分せよ。
【解答例】
両辺5乗して, ![]()
![]() で微分すると,
で微分すると, ![]()
![Rendered by QuickLaTeX.com \begin{array}{lll}\dfrac{dy}{dx}&=&\dfrac{1}{\dfrac{dx}{dy}}\\&=&\dfrac{1}{5y^4}\\&=&\dfrac{1}{5\left(\sqrt[5]{x}\right)^4}\\&=&\dfrac{1}{5\sqrt[5]{x^4}}\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-bc06ec0f63b2a0c6f7dcc13d059b1ffc_l3.png)
【別解】この程度の問題であれば, 上記方法をとるより, ![]() として, 普通に微分を行った方が早い。
として, 普通に微分を行った方が早い。![Rendered by QuickLaTeX.com \begin{array}{lll}y'&=&\dfrac15x^{\frac15-1}\\&=&\dfrac15x^{-\frac45}\\&=&\dfrac{1}{5\sqrt[5]{x^4}}\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-896f7d5a402f2f905e1f50e2ddc94793_l3.png)
【![]() の例】関数
の例】関数![]() を微分せよ。
を微分せよ。
【解答例】![]() で微分すると,
で微分すると, ![]() となるので,
となるので, 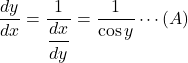
ここで, ![]() から,
から, ![]() となり,
となり, ![]() であるので,
であるので, ![]()
したがって, ![]()
これを![]() に代入すると,
に代入すると, ![]()
となる。
よって, ![]()
逆関数の微分法
逆関数の微分を使う場面は, ![]() 逆関数をとった方が楽な場合, つまり,
逆関数をとった方が楽な場合, つまり, ![]() を
を![]() とした方がよい場合。
とした方がよい場合。![]()
![]() の形で表せない場合に用いるとよい。
の形で表せない場合に用いるとよい。
ただ, 上の![]() の例題のように, 場合によってはそのままやった方が早い場合もある。
の例題のように, 場合によってはそのままやった方が早い場合もある。
 数樂管理人のブログ
数樂管理人のブログ 

