こんにちは。それではやっていきましょう。
四面体![]() において,
において, ![]() ,
, ![]() ,
, ![]() ,
, ![]() であり, 辺
であり, 辺![]() の中点を
の中点を![]() とする。このとき, 次の問いに答よ。
とする。このとき, 次の問いに答よ。
(1) 辺![]() の長さを求めよ。
の長さを求めよ。
(2) 辺![]() の長さを求めよ。
の長さを求めよ。
(3) ![]() の大きさを求めよ。
の大きさを求めよ。
(4) 四面体![]() の体積を求めよ。
の体積を求めよ。
【解答例】
(1) ![]() は直角二等辺三角形なので,
は直角二等辺三角形なので, ![]() (答)
(答)
(2) ![]() は
は![]() の二等辺三角形だから,
の二等辺三角形だから, ![]() ,
, ![]() ,
,
よって, 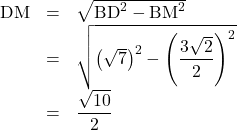
![]() (答)
(答)
(3) ![]() は
は![]() の直角二等辺三角形だから,
の直角二等辺三角形だから, ![]() ,
, ![]() で余弦定理より,
で余弦定理より, 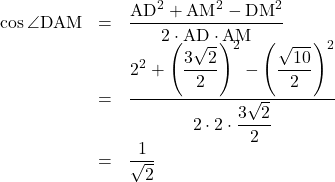
よって, ![]() (答)
(答)
(4) 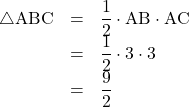
底面を![]() としたとき, 高さは
としたとき, 高さは![]() なので,
なので, ![]()
よって, 求める体積は, ![]() (答)
(答)
 数樂管理人のブログ
数樂管理人のブログ 


