こんにちは。今回の基礎学ですが, 難しかったですか?難しいと見えた方は練習量が足りていないんでしょうね。ここのサイトで繰り返し練習を積んでみてください。今回は平面図形の問題を解説してみたいと思います。
下の図の, ![]() は
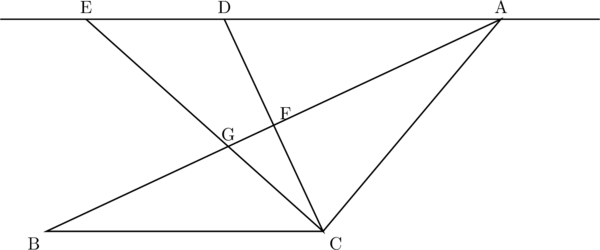
は![]() の二等辺三角形である。点Aを通り辺BCに平行な直線をひき, その直線上に
の二等辺三角形である。点Aを通り辺BCに平行な直線をひき, その直線上に![]() となる点D,
となる点D, ![]() となる点Eをとる。
となる点Eをとる。
点Cと点D, Eをそれぞれ結び, CDとAB, CEとABとの交点をそれぞれF, Gとする。
次の(1)~(3)に答えなさい。
(1)
(2)
(3) 点Eと点Bを結ぶ。
【2023年徳島県中3第2回基礎学力テスト】
(1) ![]() と
と![]() で
で
仮定より, ![]()
![]() より, 錯角は等しいので,
より, 錯角は等しいので, ![]()
![]()
![]() より,
より,
1組の辺とその両端の角がそれぞれ等しいので, ![]()
(2)
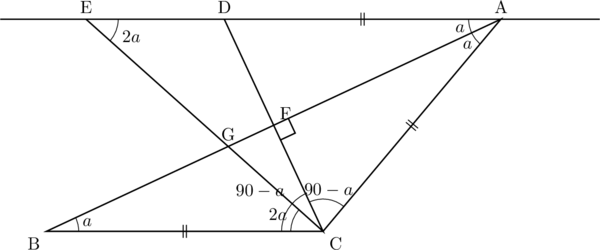
これより,
ここで
また,
直線CFは頂角の二等分線である。
したがって,
(3)
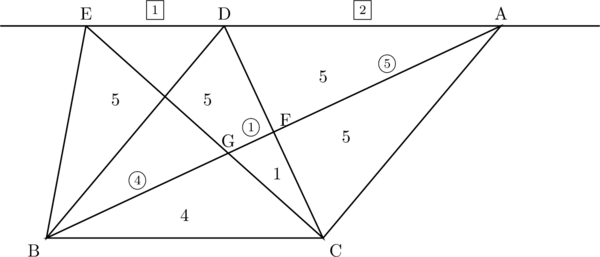
EとB, DとBを結ぶ。
(2)から四角形ACBDはひし形である。したがって, 対角線で区切られた4つの三角形の面積はすべて等しい。また, 対角線はそれぞれの中点で交わる。
したがって,
以上より, 四角形BCAEは25,
25倍
 数樂管理人のブログ
数樂管理人のブログ 



解説がわかりにくい
少し編集を変えてみました。