高校数学：数III微分：a^bとb^a(0＜a＜b)の大小関係について

こんにちは。頻出系ですかね。それではいってみましょう。

問題

【問題】異なる正の実数 $a, b$ について, $a^b$ と $b^a\ (0<a<b)$ の大小関係を考える。
(1) $f(x)=\dfrac{\log x}{x}$ のグラフを考えることにより, $e^{\pi}$ と $\pi^e$ の大小関係を調べよ。
(2) $a^b$ と $b^a$ の大小関係を次の場合において答えよ。
( $\,$ i $\,$ ) $0<a<b\leqq e$
( $\,$ ii $\,$ ) $e\leqq a<b$
(3) $2^{\pi}$ と $\pi^2$ の大小関係を調べよ。

解答・解説例

【予備知識】
まず, $a^b, b^a$ を比較するのに, $\dfrac{\log x}{x}$ が出てくるのはなぜだろうという疑問が生じるかもしれない。
そこで,
$a^b$ と $b^a$ をイコールで結んでみることにすると,
$a^b=b^a$
両辺 $\dfrac{1}{ab}$ 乗すると,
$a^{\frac1a}=b^{\frac1b}$ となる。
この両辺の自然対数をとると,
$\dfrac{\log a}{a}=\dfrac{\log b}{b}$
となって, $\dfrac{\log x}{x}$ の大小関係で比較ができるという仕組みになっている。
【解答例】
(1)
$f'(x)=\dfrac{1-\log x}{x^2}$
$f'(x)=0$ となるのは, $x=e$ のとき,
$\begin{array}{|c||c|c|c|c|} \hline x &0& \cdots & e & \cdots \\ \hline f'(x) & & + & 0 & - \\ \hline f(x) & & \nearrow &\dfrac1e & \searrow \\ \hline\end{array}$
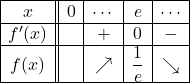
グラフを書くと以下のようである。

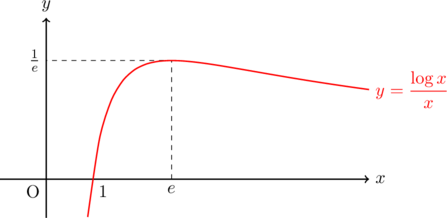
このとき, $0<x\leqq e$ でグラフは単調増加, $e\leqq x$ でグラフは単調減少を表す。
よって,
$\dfrac{\log e}{e}>\dfrac{\log\pi}{\pi}$
よって,
$\pi\log e>e\log\pi$
よって, $e^{\pi}>\pi^e$
単純に【予備知識】示し, グラフから
$e<\pi$ なので値が大きい方が小さいことになる。
よって, $e^{\pi}>\pi^e$ としてもよいと思う。
(2)
( $\,$ i $\,$ )(1)より, グラフは単調増加であるから, 値が大きい方が大きい。
$a<b$ より, $a^b<b^a$
( $\,$ ii $\,$ )(1)より, グラフは単調減少であるから, 値が小さい方が大きい。
$a<b$ より, $a^b>b^a$
(3)
$2<e<\pi$ であるから, $(2)$ が使えなさそうに見えるが, 2乗することでそれを回避する。
$2^{\pi}$ と $\pi^2$ を2乗すると,
$4^{\pi}$ , $\pi^4$ となり, これで(2)が使える。
$e<\pi<4$ なので,
$4^{\pi}<\pi^4$
よって, $2^{\pi}<\pi^2$

問題

解答・解説例

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル