こんにちは。似たようなことは平面ベクトルでやっています。それの空間版と思っていただくといいと思います。式変形の方法に慣れてください。
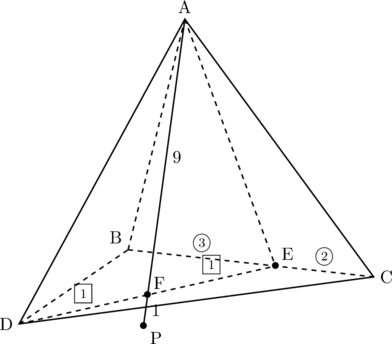
【問題】四面体ABCDと点Pが次の関係を満たしているとき, 点Pは四面体の内部にあるか, 外部にあるか示せ。![]()
【解答・解説】![]() ,
, ![]() ,
, ![]() ,
, ![]() とおくと,
とおくと,
与式は次のようになる![]()
これを![]() について解いていくと,
について解いていくと, ![]()
![]()
さらにこれを変形していくと, 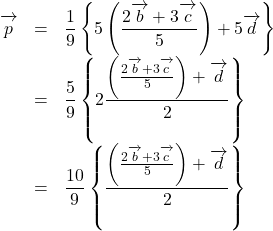
となる。
上記式中の![]() から
から![]() を
を![]() に内分する点をEとして,
に内分する点をEとして, ![]() を
を![]() とすると,
とすると, ![]() なので,
なので, 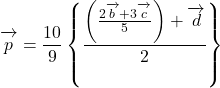
は, 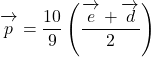
と書け, これより, ![]() を
を![]() に内分する点をFとすると,
に内分する点をFとすると, ![]() となり,
となり, ![]() は
は![]() を
を![]() 倍したものなので,
倍したものなので, ![]() となる。また, これより, 点Pは
となる。また, これより, 点Pは![]() を
を![]() に外分した点である。
に外分した点である。
したがって, 点Pは四面体の外部にある。
 数樂管理人のブログ
数樂管理人のブログ 


