TikZ：高校数学：数III積分：面積の2等分問題(青山学院大学)

こんにちは。比較的有名な問題だと思います。早速いってみましょう。

青山学院大学

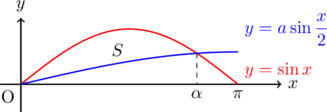
【問題】曲線 $y=\sin x\,$ $(0\leqq x\leqq\pi)$ と $x$ 軸とで囲まれる部分の面積を, 曲線 $y=a\sin\dfrac{x}{2}\,$ $(a>0)$ によって2等分するためには, 定数 $a$ の値をいくらにすればよいか。
【青山学院大学】

解答・解説

【解答・解説】

※ポイント
まず, 2つの曲線の交点を具体的に求めることはできないので, 交点の $x$ 座標を $\alpha$ とおいて, $\alpha$ が絡む式を導きます。その関係式を後々使って解法に結び付けます。
交点の $x$ 座標を $\alpha$ とおくと,
$\sin \alpha=a\sin\dfrac{\alpha}{2}$
※ポイント2
2 $\sin \alpha=2\sin\dfrac \alpha2\cos\dfrac \alpha2\,$ (倍角の公式から得られる)を用いると,
$2\sin\dfrac \alpha2\cos\dfrac \alpha2-a\sin\dfrac \alpha2=0$ 　
$\sin\dfrac \alpha2\left(2\cos\dfrac \alpha2-a\right)=0$
から,
$\cos\dfrac \alpha2=\dfrac a2$ という関係式を得る。
ここで $\sin x$ を $0\leqq x\leqq \pi$ で積分して面積を求めると,
$\begin{array}{lll}\displaystyle\int_0^\pi\sin x\, dx&=&\left[-\cos x\right]_0^\pi\\&=&1-(-1)\\&=&2\end{array}$
面積が2等分されるということは, 2つの曲線に囲まれた部分の面積 $S$ が1になればよい。
したがって,
$S=\displaystyle\int_0^{\alpha}\left(\sin x-a\sin\dfrac x2\right)\, dx=1$
であればよい。
これを計算していくと,
$\begin{array}{lll}S&=&\left[-\cos x+2a\cos\dfrac x2\right]_0^{\alpha}\cdots\textcircled{\scriptsize{1}}\\&=&\left[-\left(2\cos^2\dfrac x2-1\right)+2a\cos\dfrac x2\right]_0^{\alpha}\\&=&-2\cos^2\dfrac\alpha2+1+2a\cos\dfrac\alpha2-(-1+2a)\cdots\textcircled{\scriptsize{2}}\\&=&-2\cdot\dfrac{a^2}{4}+1+2a\cdot\dfrac a2+1-2a\\&=&\dfrac{a^2}{2}-2a+2=1\end{array}$
※ポイント3
$\maru1$ で $\cos x=2\cos^2\dfrac x2-1\,$ (倍角の公式から得られる)を用いている。
$\maru2$ では, 初めに求めた $\cos\dfrac \alpha2=\dfrac a2$ を代入している。
これから,
$\dfrac{a^2}{2}-2a+1=0$
$a^2-4a+2=0$
これを解いて,
$a=2\pm\sqrt2$
$\dfrac a2=\cos\dfrac\alpha2<1$ であるから, $a<2$
よって, $a=2-\sqrt2\cdots$ (答)

青山学院大学

解答・解説

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル