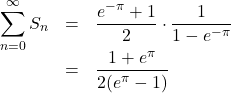こんにちは。早速いってみましょう。
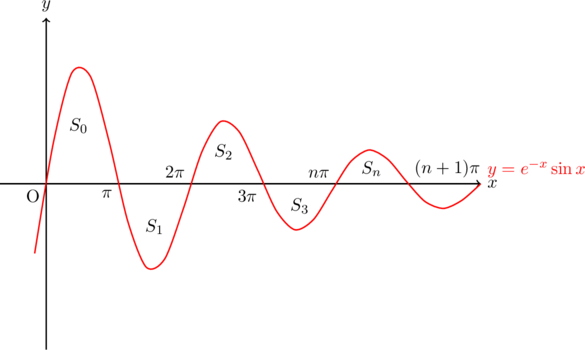
曲線![]() と
と![]() 軸との交点を原点Oから正の方向に順に
軸との交点を原点Oから正の方向に順に![]() ,
, ![]() ,
, ![]() ,
, ![]() とする。
とする。
(1) この曲線と線分![]() とで囲まれた部分の面積
とで囲まれた部分の面積![]() を求めよ。
を求めよ。
(2) ![]() を求めよ。
を求めよ。
【東京女子大】
【解答・解説】
求める面積は
したがって,
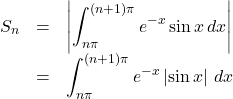
また,
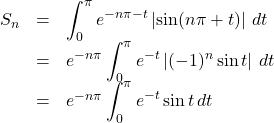
これは
ここで,
![Rendered by QuickLaTeX.com \begin{array}{lll}S_0&=&\displaystyle\int\left(-e^{-t}\right)'\sin t\, dt\\&=&\left[-e^{-t}\sin t\right]_0^{\pi}+\displaystyle\int_0^{\pi} e^{-t}\cos t\, dt\\&=&\displaystyle\int_0^{\pi} e^{-t}\cos t\, dt\\&=&\left[-e^{-t}\cos t\right]_0^{\pi}-\displaystyle\int_0^{\pi}e^{-t}\sin t\, dt\\&=&e^{-\pi}+1-S_0\end{array}](https://mathtext.info/blog/wordpress/wp-content/ql-cache/quicklatex.com-083549ed53f2b7b8860ca9e6fa178231_l3.png)
これより,
(2)
よって,
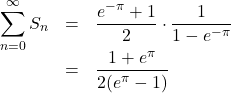
このように減衰曲線では, 面積は等比数列になり, その無限級数和は収束します。
こんにちは。早速いってみましょう。
曲線![]() と
と![]() 軸との交点を原点Oから正の方向に順に
軸との交点を原点Oから正の方向に順に![]() ,
, ![]() ,
, ![]() ,
, ![]() とする。
とする。
(1) この曲線と線分![]() とで囲まれた部分の面積
とで囲まれた部分の面積![]() を求めよ。
を求めよ。
(2) ![]() を求めよ。
を求めよ。
【東京女子大】
【解答・解説】

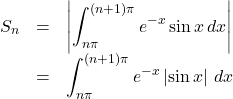
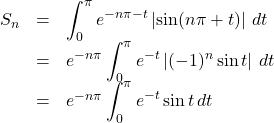
![Rendered by QuickLaTeX.com \begin{array}{lll}S_0&=&\displaystyle\int\left(-e^{-t}\right)'\sin t\, dt\\&=&\left[-e^{-t}\sin t\right]_0^{\pi}+\displaystyle\int_0^{\pi} e^{-t}\cos t\, dt\\&=&\displaystyle\int_0^{\pi} e^{-t}\cos t\, dt\\&=&\left[-e^{-t}\cos t\right]_0^{\pi}-\displaystyle\int_0^{\pi}e^{-t}\sin t\, dt\\&=&e^{-\pi}+1-S_0\end{array}](https://mathtext.info/blog/wordpress/wp-content/ql-cache/quicklatex.com-083549ed53f2b7b8860ca9e6fa178231_l3.png)