こんにちは。R6年度徳島県の高校入試の数学の平面図形の問題の解説です。それではどうぞ。
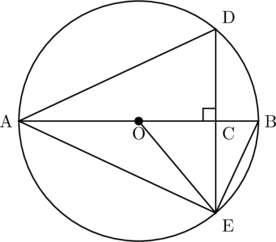
下の図のように, 円Oの直径AB上に点Cをとり, 点Cを通り直径ABに垂直な直線と円Oとの交点をそれぞれD, Eとする。中心Oと点E, 点Aと点D, 点Aと点E, 点Bと点Eをそれぞれ結ぶ。(1)~(4)に答えなさい。
(1)
(2)
(a)
【
ACは共通だから,
仮定より,
また, 直径ABは弦DEの垂直二等分線だから,
(b) (a)で示したことを用いて,
(3)
(4)
(1) 半円の弧に対する円周角なので![]() (答)
(答)
(2) (a) ![]() の条件から
の条件から
2組の辺とその間の角![]() (答)
(答)
(b) ![]() と
と![]() で,
で, ![]() の円周角より,
の円周角より, ![]()
![]() より,
より,![]()
![]() の中心角と円周角の関係より,
の中心角と円周角の関係より, ![]()
![]() より,
より, ![]()
![]() より,
より,
2組の角がそれぞれ等しいので, ![]() ∽
∽![]()
(3) 相似比が![]() なので, 面積比は
なので, 面積比は![]() 。
。![]() の面積が50cm
の面積が50cm![]() なので,
なので, ![]() の面積を
の面積を![]() として求めると,
として求めると, ![]()
![]() なので, 求める面積は,
なので, 求める面積は, ![]()
![]() (答)
(答)
(4) ![]() ∽
∽![]() であり, 相似比は
であり, 相似比は![]() である。このとき,
である。このとき, ![]() , かつ,
, かつ, ![]() である。ここで,
である。ここで, ![]() であるが, 比の割合が, それぞれ,
であるが, 比の割合が, それぞれ, ![]() と
と![]() で異なるので, それを合わせるために
で異なるので, それを合わせるために![]() の方を
の方を![]() 倍すると,
倍すると, ![]() となる。このとき,
となる。このとき, ![]() となるので,
となるので, ![]() (答)
(答)
同じ長さなのに比がそろっていない。
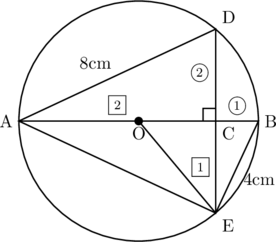
比をそろえると,
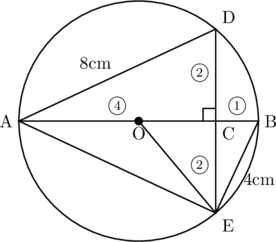
 数樂管理人のブログ
数樂管理人のブログ 


