こんにちは。令和6年度の徳島県の入試問題から, 一次関数の問題です。
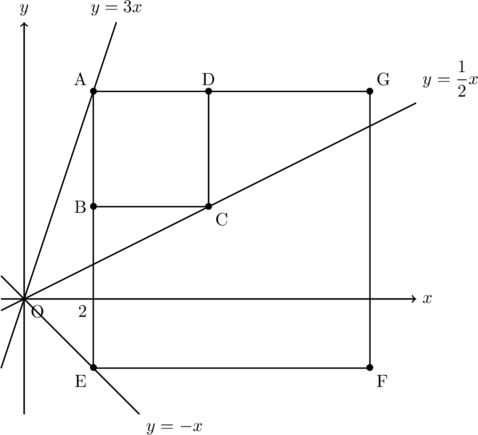
下の図のように, 直線![]() 上に点A, 直線
上に点A, 直線![]() 上に点C, 直線
上に点C, 直線![]() 上に点Eがあり, 点Aの
上に点Eがあり, 点Aの![]() 座標は3である。また, 四角形ABCDと四角形AEFGがともに正方形になるように点B, D, F, Gをとる。ただし, 点Cと点Fの
座標は3である。また, 四角形ABCDと四角形AEFGがともに正方形になるように点B, D, F, Gをとる。ただし, 点Cと点Fの![]() 座標はともに3より大きく, 辺ABと辺AEはともに
座標はともに3より大きく, 辺ABと辺AEはともに![]() 軸に平行とする。(1)~(4)に答えなさい。
軸に平行とする。(1)~(4)に答えなさい。
(1) 点Eの座標を求めなさい。
(2) 2点A, Fを通る直線の式を求めなさい。
(3) 正方形ABCDを, 辺ABを回転の軸として1回転させてできる立体の体積を求めなさい。
(4) 辺FG上に点Pをとり, ![]() の周の長さが最小となるような点Pの座標を求めなさい。
の周の長さが最小となるような点Pの座標を求めなさい。
(1) ![]() を
を![]() に代入して,
に代入して, ![]() 。
。
よって, ![]() (答)
(答)
(2) 線分AFは正方形の対角線なので, ![]() の増加量と
の増加量と![]() の増加量は等しく, 右下がりになっているので, 直線AFの傾きは
の増加量は等しく, 右下がりになっているので, 直線AFの傾きは![]() である。したがって, 求める直線は
である。したがって, 求める直線は![]() とおくことができ, A(3, 9)を通るので, これを代入し, 切片
とおくことができ, A(3, 9)を通るので, これを代入し, 切片![]() を求めると,
を求めると, ![]()
よって, 求める直線は![]() (答)
(答)
【別解】A(3, 9), E(3, -3)より, ![]() であるから,
であるから, ![]() ,
, ![]() である。よって求める直線は, A(3, 9),
である。よって求める直線は, A(3, 9), ![]() を通る直線
を通る直線![]()
(3) 回転させたときにできる立体の底面の半径と高さを求めるために, (2)でもとめた直線![]() と
と![]() の交点Cの座標を求める。
の交点Cの座標を求める。![]() ,
, ![]() を
を![]() に代入して
に代入して![]() 。よって, C( 8, 4 )となる。このことから,
。よって, C( 8, 4 )となる。このことから, ![]() なので, 求める立体の体積は,
なので, 求める立体の体積は, ![]()
![]() (答)
(答)
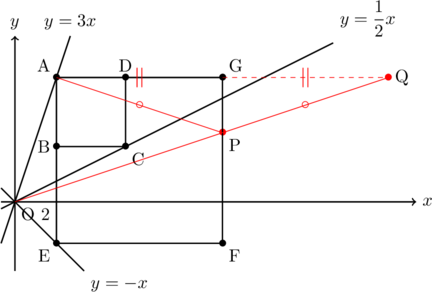
(4) 直線GFについて, Aと対称になる点Qをとる。![]() なので,
なので, ![]() 。よって, 直線OQの式は
。よって, 直線OQの式は![]() 。求める点Pは直線OQと線分GFの交点だから,
。求める点Pは直線OQと線分GFの交点だから, ![]() に
に![]() を代入して,
を代入して, ![]() 。
。
よって, 点Pの座標は, ![]() (答) 下図参照
(答) 下図参照
 数樂管理人のブログ
数樂管理人のブログ 


