こんにちは。定期テストでよく問われる問題ですね。それではどうぞ。
【問題】点( 3, 4 )を, 原点Oを中心として![]() だけ回転させた点Qの座標を求めよ。
だけ回転させた点Qの座標を求めよ。
点Pの動径![]() は
は![]() である。したがって, 線分OPと
である。したがって, 線分OPと![]() 軸の正の向きがなす角を
軸の正の向きがなす角を![]() とすると,
とすると, ![]() ,
, ![]() である。このことから, 点Pを
である。このことから, 点Pを![]() ,
, ![]() ,
, ![]() を用いて表すと,
を用いて表すと, ![]() となる。
となる。
これを![]() 回転させると,
回転させると, ![]() 座標は
座標は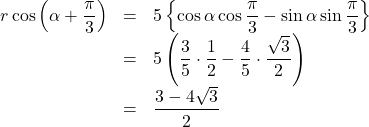
![]() 座標は,
座標は, 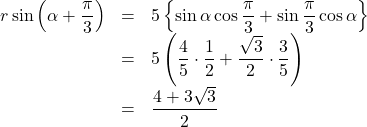
よって求めるQの座標は, 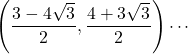 (答)
(答)
こんにちは。定期テストでよく問われる問題ですね。それではどうぞ。
【問題】点( 3, 4 )を, 原点Oを中心として![]() だけ回転させた点Qの座標を求めよ。
だけ回転させた点Qの座標を求めよ。
点Pの動径![]() は
は![]() である。したがって, 線分OPと
である。したがって, 線分OPと![]() 軸の正の向きがなす角を
軸の正の向きがなす角を![]() とすると,
とすると, ![]() ,
, ![]() である。このことから, 点Pを
である。このことから, 点Pを![]() ,
, ![]() ,
, ![]() を用いて表すと,
を用いて表すと, ![]() となる。
となる。
これを![]() 回転させると,
回転させると, ![]() 座標は
座標は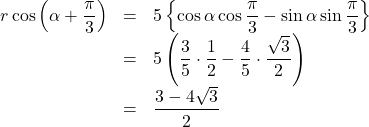
![]() 座標は,
座標は, 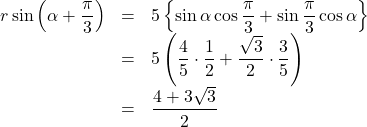
よって求めるQの座標は, 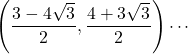 (答)
(答)