こんにちは。相城です。方程式を違った角度から見てみようというのが今回の目標です。それではどうぞ。
中1の方程式
![]() という方程式
という方程式
この場合、左辺の![]() と右辺の
と右辺の![]() が釣り合う(等しい)
が釣り合う(等しい)![]() の値を求める。
の値を求める。
![]()
中2の連立方程式
文字を1つ消去して次元を下げる。その方法に
(i)加減法、(ii)代入法がある。
ここでは、グラフ的見方で捉えてみます。![]()
二元一次方程式⇒(変形)⇒![]() 一次関数
一次関数
結論から言うと二元一次方程式![]() と一次関数
と一次関数![]() は同じである。
は同じである。![]() を変形すると
を変形すると![]() の一次関数の直線の式が得られる。その直線上の点、 すなわち直線の座標
の一次関数の直線の式が得られる。その直線上の点、 すなわち直線の座標![]() はすべて
はすべて![]() を満たす。すなわち
を満たす。すなわち![]() の座標
の座標![]() は
は![]() を満たす。よって
を満たす。よって![]() の解の集合も直線を表す。
の解の集合も直線を表す。
連立方程式とは、異なる2直線の交点を求める作業なのである。
図1は以下の普通の連立方程式を表す。
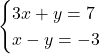
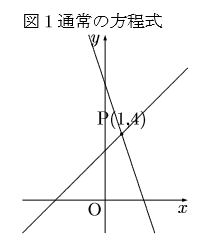
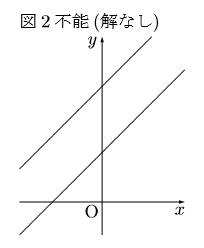
連立方程式の定数項(一次関数でいう切片)が違うだけの場合を不能(図2)という。
不能(解なし)
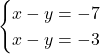
連立方程式の2式が同値の場合は不定(図3)という。
不定(解無数)
ただ、不定でも![]() など
など![]() とおける場合は、 その解を
とおける場合は、 その解を![]() として扱う場合がある。ただ中学生ではその扱いはしない? と思うのでここでは紹介だけにとどめておく。
として扱う場合がある。ただ中学生ではその扱いはしない? と思うのでここでは紹介だけにとどめておく。
中3の二次方程式
解法 (i)因数分解、(ii)平方完成、(**)解の公式がある。
二次方程式の一般式は次式で与えられる。
![]()
ここでこの解は、解の公式より次式で与えられる。
![]()
方程式的見方
まず左辺を平方完成させて変形していくと
両辺
これで
中学生では、二次方程式
補足(グラフ的解釈)
詳しくは高校生で学習してください。
もちろん二次方程式で、
ここでは中学生の範囲を超えてグラフの交点として考えてみます。
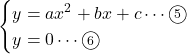
ここで
となり、グラフに表すと図4のようになる。ここでは
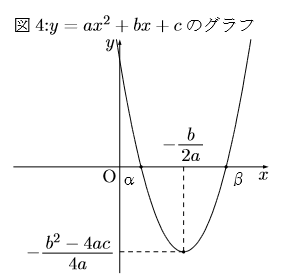
この![]() (二次関数)と
(二次関数)と![]() (
(![]() )との交点が、解の公式
)との交点が、解の公式![]() で与えられるものそのものである。
で与えられるものそのものである。
また、解の公式の根号中の![]() が次のようになると、解の個数が分かる。
が次のようになると、解の個数が分かる。
![]() 解2個(
解2個(![]() 軸との交点が2個存在)
軸との交点が2個存在)
![]() 解1個(
解1個(![]() 軸と接する。交点が1個存在)
軸と接する。交点が1個存在)
![]() 解0個(
解0個(![]() 軸とは交わらない。実数解は存在しない)
軸とは交わらない。実数解は存在しない)
またグラフの頂点を見ても分かるように、![]() なら
なら![]() とも併せて、頂点の
とも併せて、頂点の![]() 座標は
座標は![]() となり、頂点は
となり、頂点は![]() より下になる。
より下になる。![]() の場合は
の場合は![]() より上になる。
より上になる。
この![]() は判別式と言ってかなり活躍するので、高校生になったらぜひ活用していただきたい。
は判別式と言ってかなり活躍するので、高校生になったらぜひ活用していただきたい。
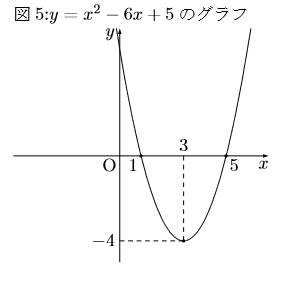
図5に![]() のグラフを書いてみました。
のグラフを書いてみました。![]() とおくと
とおくと![]() となる。グラフ的な見方を利用すると、中1の方程式
となる。グラフ的な見方を利用すると、中1の方程式![]() を考えると、実は2直線
を考えると、実は2直線![]() の交点の
の交点の![]() 座標だったりするのですね。面白いものです。
座標だったりするのですね。面白いものです。
 数樂管理人のブログ
数樂管理人のブログ 

