こんにちは。相城です。今回はメネラウスの定理とその証明を見ていきましょう。
メネラウスの定理
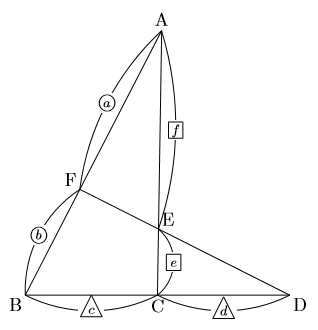
下の図の△ABCで, 点F, EはそれぞれAB,AC上の点で, BCの延長線とFEの延長線の交点をDとします。このとき,
![]()
が成り立つ。この定理をメネラウスの定理という。
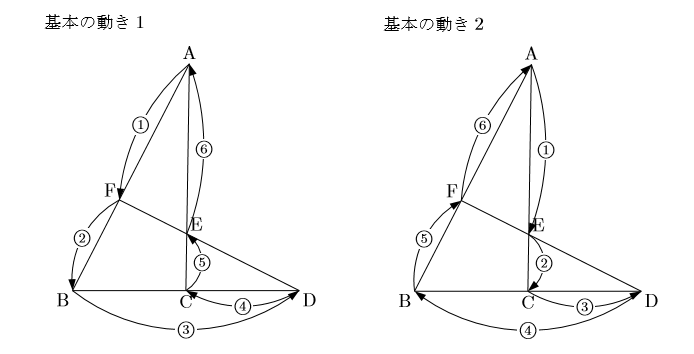
基本の動き方 ①→②→③→④→⑤→⑥の順で動きます。
証明
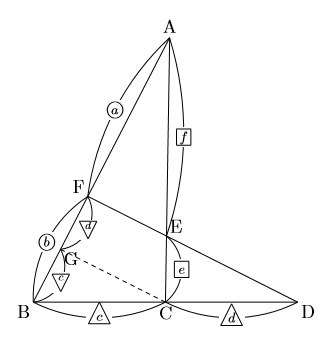
Cを通り、FDに平行な直線とABの交点をGとする。
CG![]() DFより, BG : GF
DFより, BG : GF![]() であるから,
であるから,  の長さを
の長さを![]() を使って表すと,
を使って表すと,
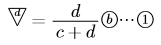
また, △AGCで, FE![]() GCであるから,
GCであるから,
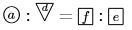
dを①で置き換えると,
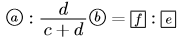
つまり,
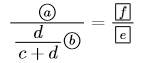
両辺を整理すると,
![]()
両辺に
![]()
ちなみに,
![]()
とも書ける。
 数樂管理人のブログ
数樂管理人のブログ 

