こんにちは。平行四辺形と面積②です。それではどうぞ。
面積比の問題で, 1つの攻略方法として, 相似比の2乗から攻める方法を紹介しておりますが, 相似な関係がない場合は, 役に立ちません。
そこで, 相似な関係がなくてもできる攻略方法を提示できればと思います。ただ, 全てにおいて攻略できるかは不明ですので, その点ご了承ください。
さて, 今回攻略法に使う, 予備知識は次の基本パターンになります。
1つの三角形の頂点を通る直線で, 2つの三角形に分けたとき, 2つの三角形の底辺の長さが, ![]() ,
, ![]() であるなら, 2つの三角形の面積比は
であるなら, 2つの三角形の面積比は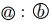 であるというものです。これを基本パターンとします。
であるというものです。これを基本パターンとします。
この関係を用いて, 攻略していくことにします。
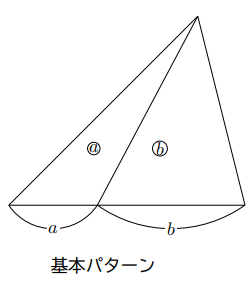
さて, 次の問題は, 相似比の2乗を用いて攻略するのに用いた問題です。
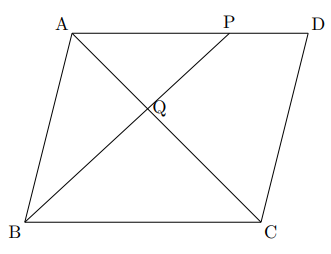
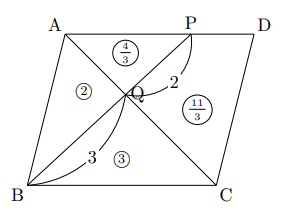
右の図で, 右の図で四角形ABCDは平行四辺形で, Pは辺ADを2 : 1に分ける点である。線分PBと線分ACの交点をQとするとき, 次の問いに答えなさい。
(1) 四角形PQCDの面積と平行四辺形ABCDの面積の比を最も簡単な整数の比で表しなさい。
ここでは, △APQ∽△CBQであり, AQ : CQ![]() 2 : 3, PQ : BQ
2 : 3, PQ : BQ![]() 2 : 3であることは, 周知の事実としてまいります。
2 : 3であることは, 周知の事実としてまいります。
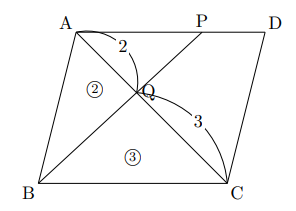
AQ : CQ![]() 2 : 3であることから, 上の面積比の関係から, △ABQと△CBQの面積比は, 基本パターンより, △ABQ : △CBQ
2 : 3であることから, 上の面積比の関係から, △ABQと△CBQの面積比は, 基本パターンより, △ABQ : △CBQ![]() ② : ③。
② : ③。
このとき, PQ : BQ![]() 2 : 3と, △ABQ
2 : 3と, △ABQ![]() ②を用いて, △APQの面積の割合をもとめると, 基本パターンより,
②を用いて, △APQの面積の割合をもとめると, 基本パターンより,
2 : 3 ![]() △APQ : ②
△APQ : ②
△APQ ![]()
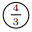 となります。
となります。
ここで, 平行四辺形ABCDの半分の面積は△ABCが⑤, ( ②![]() ③ )であることから, △ADCも⑤, △APQ
③ )であることから, △ADCも⑤, △APQ![]()
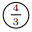 より,
より,
四角形PQCD![]() ⑤
⑤![]()
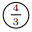
![]()
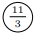
よって, 求める面積比は,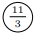 : ⑤
: ⑤![]() 2
2
となり, 整数比にするため, 3倍して,
11 : 30
となります。
これで, この方法でもきちんと解くことができることがわかります。
これのメリットは, 相似系がなくても対応できるところです。
デメリット?は分数がよく出てくるところでしょうか。。。?
次には, 相似系のないものを解いてみます。
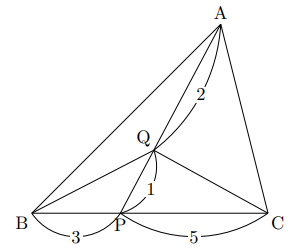
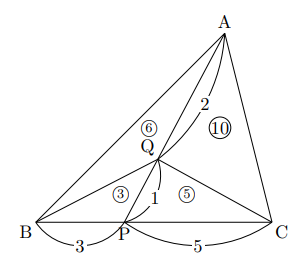
右の△ABCで, 辺BCを3 : 5に分ける点をP, APを2 : 1に分ける点をQとします。
このとき, 次の面積比を最も簡単な整数の比で表しなさい。
(1) △QBP : △QCP
(2) △AQB : △AQC
(3) △QBP : △ABC
このような問題では, 見た目でもいいので, 一番小さい三角形を基準に考えていけばいいことが多い。
本質が見えてくると, 一番小さい三角形を①とすれば事足りてきます。
ここでは, そういうやり方でなくとも, 一番最初の基本パターンから攻めることで, 解けることを実証したいと思います。
ただし, 一番小さい三角形に注目することに変わりはありません。ここでは△QBPが一番小さく, △QBPと△QCPの面積比が, 基本パターンより③ : ⑤( 3 : 5 )と分かります。
次に△AQBと△QBPの面積比が, 基本パターンより, 2 : 1であり, △QBP![]() ③であるから,
③であるから,
△AQB : ③ = 2 : 1
△AQB![]() ⑥
⑥
同様に,
△AQC : ⑤ ![]() 2 : 1
2 : 1
△AQC ![]() ⑩
⑩
となります。
これで, △ABCの中にある三角形の面積の割合がすべてわかりました。
(1)の答えは
3 : 5・・・(答)
(2)の答えは
6 : 10![]() 3 : 5・・・(答)
3 : 5・・・(答)
(3)の答えは, △ABC![]() となるので,
となるので,
3 : 24![]() 1 : 8・・・(答)
1 : 8・・・(答)
どれを基準にしていいかわからないときは, 図の中で,一番小さい三角形を選んで, 基本パターンに持ち込んだ方がよいですね。
相似比の2乗から入る問題も基本パターンで解けますからね。こちらの方が汎用性はあるかもです。ではでは。
 emath:中学数学:攻略法:平行四辺形と面積①
emath:中学数学:攻略法:平行四辺形と面積①  emath:中学数学:平行四辺形と面積比(公式編)
emath:中学数学:平行四辺形と面積比(公式編) 数樂管理人のブログ
数樂管理人のブログ 
