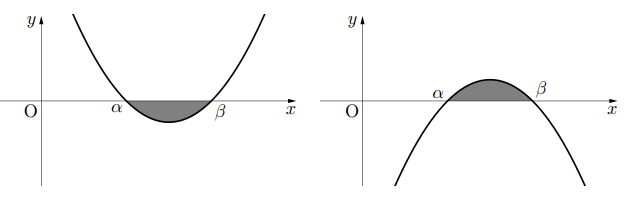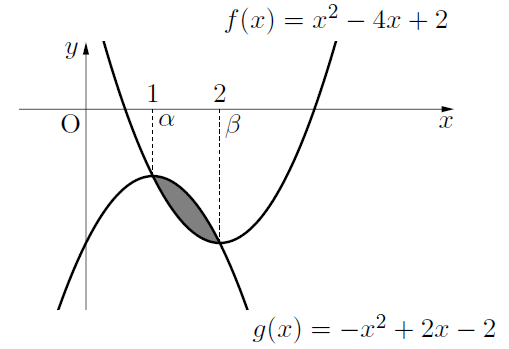こんにちは。相城です。今回は![]() 公式についてです。使えると便利ですので是非マスターしてください。
公式についてです。使えると便利ですので是非マスターしてください。
積分区間が![]() において,
において, ![]() についての2次式が
についての2次式が![]() と因数分解できるとき,
と因数分解できるとき, ![]()
が成り立つという公式である。
![]() 公式の出番の主な場面を3つ紹介する。
公式の出番の主な場面を3つ紹介する。
【公式の出番①】
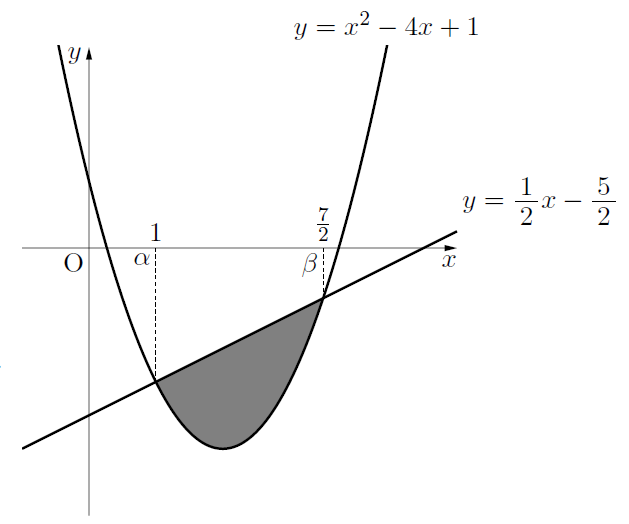
下図のように, 直線![]() と2次関数
と2次関数![]() が2点A, Bで交わり, 2点A, Bの
が2点A, Bで交わり, 2点A, Bの![]() 座標が
座標が![]() とする。このとき, 色のついた部分の面積を求めるのに用いる。
とする。このとき, 色のついた部分の面積を求めるのに用いる。

【公式の出番②】
下図のように, 2次関数![]() と2次関数
と2次関数![]() が2点A, Bで交わり, 2点A, Bの
が2点A, Bで交わり, 2点A, Bの![]() 座標が
座標が![]() とする。このとき, 色のついた部分の面積を求めるのに用いる。
とする。このとき, 色のついた部分の面積を求めるのに用いる。

【公式の出番③】
下図のように, ![]() の係数が等しい3次関数
の係数が等しい3次関数![]() と, 3次関数
と, 3次関数![]() が2点A, Bで交わり, 2点A, Bの
が2点A, Bで交わり, 2点A, Bの![]() 座標が
座標が![]() とする。このとき, 色のついた部分の面積を求めるのに用いる。
とする。このとき, 色のついた部分の面積を求めるのに用いる。

出番①, ②, ③について,
①
②
③
という具合に因数分解できるはずである。
このことに着目すると, 求める面積
出番①を例に
![Rendered by QuickLaTeX.com \begin{array}{lll}S&=&\displaystyle\int_{\alpha}^{\beta} \left\{(mx+n)-(ax^2+bx+c)\right\}\, dx\\&=&\displaystyle\int_{\alpha}^{\beta} -a(x-\alpha)(x-\beta)\,dx \\&=&-a \displaystyle\int_{\alpha}^{\beta} (x-\alpha)(x-\alpha+\alpha-\beta)\,dx\\&=&-a \displaystyle\int_{\alpha}^{\beta} \left\{(x-\alpha)^2+(\alpha-\beta)(x-\alpha)\right\}\,dx\\&=&-a \left[\dfrac13 (x-\alpha)^3+\dfrac12 (\alpha-\beta)(x-\alpha)^2\right]_{\alpha}^{\beta}\\&=&-a \left\{ \dfrac13 (\beta-\alpha)^3+\dfrac12 (\alpha-\beta)(\beta-\alpha)^2\right\}\\&=&-a \left\{ \dfrac13 (\beta-\alpha)^3-\dfrac12 (\beta-\alpha)^3\right\}\\&=&\dfrac{a}{6}(\beta-\alpha)^3\end{array}](https://mathtext.info/blog/wp-content/ql-cache/quicklatex.com-9bfe1fd0abffcb53da14b45455697ce1_l3.png)
今回は![]() (イメージとしては上左図)でやってみたが,
(イメージとしては上左図)でやってみたが, ![]() (イメージとしては上右図)の場合も同様にできるので, 証明は割愛する。出番②に関しても, 2つの放物線の交点を求めるのに,
(イメージとしては上右図)の場合も同様にできるので, 証明は割愛する。出番②に関しても, 2つの放物線の交点を求めるのに, ![]() と因数分解できるなら, 上と同じ証明で説明ができるので, これも割愛する。
と因数分解できるなら, 上と同じ証明で説明ができるので, これも割愛する。
したがって, ![]() ,
, ![]() の場合を考慮して, 以下の公式が得られる。
の場合を考慮して, 以下の公式が得られる。![]()
実際に問題でやってみる。
この公式の出番①の例題
【例題】直線![]() と, 曲線
と, 曲線![]() で囲まれる面積を求めなさい。
で囲まれる面積を求めなさい。
【解法】
求める面積![]() は
は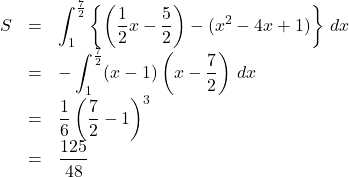
答えだけなら,単純に![]()
で求まる。![]() (答)
(答)
この公式の出番②の例題
【例題】2つの放物線![]() で囲まれる面積を求めなさい。
で囲まれる面積を求めなさい。
【解法】![]() として, 交点を求めると,
として, 交点を求めると,![]()
![]()
![]()
![]()
したがって,求める面積![]() は
は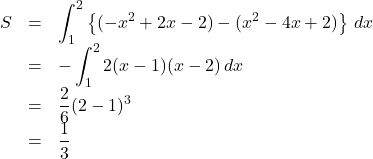
答えだけなら,単純に![]()
で求められる。![]() (答)
(答)
 数樂管理人のブログ
数樂管理人のブログ