こんにちは。相城です。今回は極座標を用いて作成しました。交点のプログラムの挙動が今一つ、つかめていません。点の記号を打つ位置が思い通りにならないことがあります。それでは問題です。
図1のように、点Oを中心とする円の周上に、3点A、B、Cがあり、![]() である。また、
である。また、![]() の大きさは90
の大きさは90![]() より大きいものとする。点Cを通り線分ABに平行な直線と円Oとの交点のうち点Cとは異なる点をDとし、線分CDについて点Aと反対側の円周上に点Eをとる。線分CDと線分AE、BEとの交点をそれぞれF、Gとし、線分AEと線分BDとの交点をHとする。このとき、次の問いに答えなさい。
より大きいものとする。点Cを通り線分ABに平行な直線と円Oとの交点のうち点Cとは異なる点をDとし、線分CDについて点Aと反対側の円周上に点Eをとる。線分CDと線分AE、BEとの交点をそれぞれF、Gとし、線分AEと線分BDとの交点をHとする。このとき、次の問いに答えなさい。
1.![]() 、
、![]() であるとき、
であるとき、![]() の大きさを求めなさい。
の大きさを求めなさい。
2.△AHB∽△FGEであることを証明しなさい。
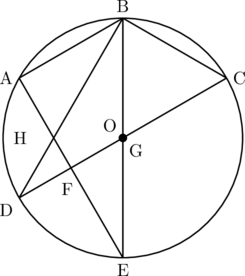
3.図2は、図1で、点Gが点Oと同じ位置となるように、4点A、B、C、Eをとったものである。円Oの半径が4cmであるとき、四角形BHFGの面積を求めなさい。
図1
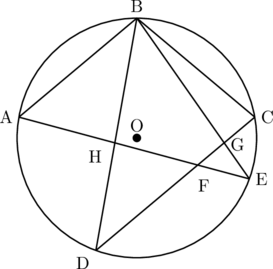
図2

答え
1.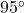
2.△AHBと△FGEで、
仮定より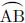

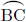 であるから
であるから
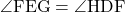 ・・・①
・・・①
CD//ABより錯角は等しいので、
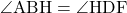 ・・・②
・・・②
①、②より
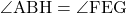 ・・・③
・・・③
対頂角は等しいので、
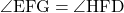 ・・・④
・・・④
CD//ABより錯角は等しいので
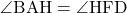 ・・・⑤
・・・⑤
④、⑤より
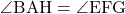 ・・・⑥
・・・⑥
③、⑥より2組の角がそれぞれ等しいので
△AHB∽△FGEである。
別: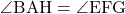 ・・・⑥
・・・⑥
はCD//ABより同位角が等しいからという理由でも可。
3.四角形BHFG=△BGD-△FDHで求める。
△BGDは頂角120 の二等辺三角形で等しい辺は半径4㎝であるから、頂角の二等分線を引きBDとの交点をPとすると、高さはGP=2m、底辺はPB
の二等辺三角形で等しい辺は半径4㎝であるから、頂角の二等分線を引きBDとの交点をPとすると、高さはGP=2m、底辺はPB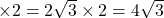 cmなので、
cmなので、
△BGD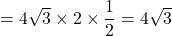 cm
cm
△FDHはFG 2cmより、FD
2cmより、FD 2cmとなるので、
2cmとなるので、 よりHF
よりHF cm(1:2:
cm(1:2: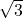 )。したがって、△FDH
)。したがって、△FDH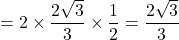 cm
cm
よって、四角形BHFG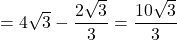 cm
cm
2.△AHBと△FGEで、
仮定より
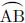
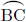 であるから
であるからCD//ABより錯角は等しいので、
①、②より
対頂角は等しいので、
CD//ABより錯角は等しいので
④、⑤より
③、⑥より2組の角がそれぞれ等しいので
△AHB∽△FGEである。
別:
はCD//ABより同位角が等しいからという理由でも可。
3.四角形BHFG=△BGD-△FDHで求める。
△BGDは頂角120
△BGD
△FDHはFG
よって、四角形BHFG
 数樂管理人のブログ
数樂管理人のブログ 

