こんにちは。相城です。さて、今回はTikZの練習に福島県の角度の問題をチョイス。図1は普通の![]() 平面の座標をつかって作図しました。図2は極座標を用いたのですが、
平面の座標をつかって作図しました。図2は極座標を用いたのですが、接点が微妙にずれてる気がするんですけどね?←実は計算間違いでした。また、点Dを通る円を描いても何か交点がおかしなところに来ちゃって・・・今一つ挙動がおかしい?(多分私の力量不足)です。では問題です。
下の図1のように、円周上の3点A、B、Cを頂点とする△ABCがありAを通る直線![]() と辺BCは平行である。ただし、AB
と辺BCは平行である。ただし、AB![]() BCである。また、
BCである。また、![]() の二等分線と辺AB、
の二等分線と辺AB、![]() との交点をそれぞれD、Eとし、線分CE上にCD
との交点をそれぞれD、Eとし、線分CE上にCD![]() EFとなる点FをとりAと結ぶ。
EFとなる点FをとりAと結ぶ。
このとき、次の(1)、(2)の問いに答えなさい。
(1) ![]() となることを証明しなさい。
となることを証明しなさい。
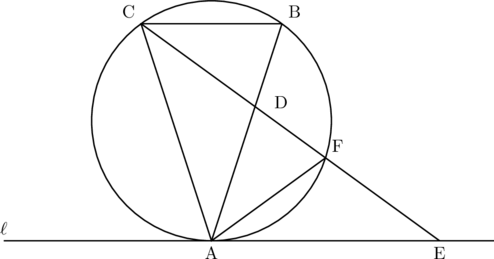
(2) 2点B、Cの位置によって、点Fの位置が変わる。下の図2のように、Fが円周上にあるとき、![]() の大きさを求めなさい。
の大きさを求めなさい。
図1
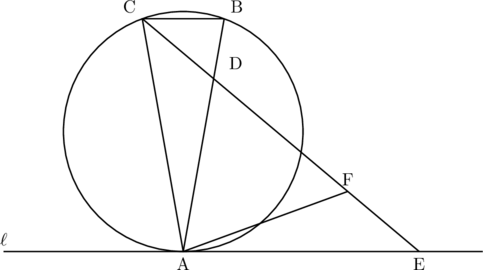
図2

答え
(1)
△ACDと△AEFで、
仮定より
CD=EF・・・①
CEは∠ACBの二等分線でAE//BCなので
錯角が等しいので
∠ACD=∠AEF・・・②
であるから△ACEは二等辺三角形なので
AC=AE・・・③
①、②、③より2組の辺とその間の角がそれぞれ等しいので
△ACD≡△AEF
よってAD=AFであるから△ADFも二等辺三角形なので、
∠AFD=∠ADF
(2)
△ABCは二等辺三角形(接点Aを通る直径は弦BCを垂直に二等分する)
∠ACD=∠BCD= とおくと円周角の定理などから
とおくと円周角の定理などから
△ABCの内角は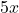 となる。
となる。
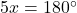 なので
なので
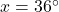
∠ABC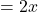 なので
なので
∠ABC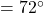
△ACDと△AEFで、
仮定より
CD=EF・・・①
CEは∠ACBの二等分線でAE//BCなので
錯角が等しいので
∠ACD=∠AEF・・・②
であるから△ACEは二等辺三角形なので
AC=AE・・・③
①、②、③より2組の辺とその間の角がそれぞれ等しいので
△ACD≡△AEF
よってAD=AFであるから△ADFも二等辺三角形なので、
∠AFD=∠ADF
(2)
△ABCは二等辺三角形(接点Aを通る直径は弦BCを垂直に二等分する)
∠ACD=∠BCD=
△ABCの内角は
∠ABC
∠ABC
 数樂管理人のブログ
数樂管理人のブログ 

