こんにちは。相城です。今回はグラフ問題です。基本問題です。数学が苦手なお子様でも確実に点数にしておきたい問題構成ですので、しっかりと身に付けてください。それではどうど。
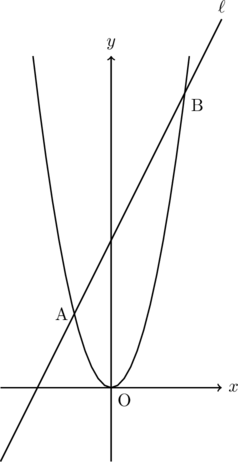
下の図のように、関数![]() のグラフと直線
のグラフと直線![]() が、2点A、Bで交わっている。Aの座標は
が、2点A、Bで交わっている。Aの座標は![]() で、Bの
で、Bの![]() 座標は2である。次の(1)~(3)の問いに答えなさい。
座標は2である。次の(1)~(3)の問いに答えなさい。
(1) ![]() の値を求めなさい。
の値を求めなさい。
(2) 直線![]() の式を求めなさい。
の式を求めなさい。
(3) △AOBの面積を求めなさい。

答え
(1) 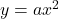 に
に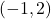 を代入して、
を代入して、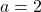 ・・・答え
・・・答え
(2) (1)より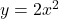 なので、これに
なので、これに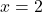 を代入してBの座標B(2, 8)を得る。よって、求める直線は2点A
を代入してBの座標B(2, 8)を得る。よって、求める直線は2点A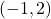 、B(2, 8)を通る直線の式。したがって、求める直線は
、B(2, 8)を通る直線の式。したがって、求める直線は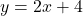 ・・・答え
・・・答え
解き方の例としては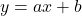 にA、Bの座標を代入して連立方程式で
にA、Bの座標を代入して連立方程式で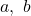 を求めるといいでしょう。
を求めるといいでしょう。
(3) (2)より直線ABの切片が4なのでこれを底辺として2つの三角形の面積の和として△AOBの面積を求めましょう。
切片の座標をPと置くと、
△AOP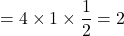
(△AOPの高さはAの 座標の絶対値である1)
座標の絶対値である1)
△BOP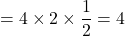
(△BOPの高さはBの 座標である2)
座標である2)
よって△AOBの面積は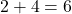 ・・・答え
・・・答え
もちろん、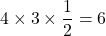 としても可
としても可
(式中の3の出どころはAの 座標の絶対値1とBの
座標の絶対値1とBの 座標2の和)
座標2の和)
(2) (1)より
解き方の例としては
(3) (2)より直線ABの切片が4なのでこれを底辺として2つの三角形の面積の和として△AOBの面積を求めましょう。
切片の座標をPと置くと、
△AOP
(△AOPの高さはAの
△BOP
(△BOPの高さはBの
よって△AOBの面積は
もちろん、
(式中の3の出どころはAの
 数樂管理人のブログ
数樂管理人のブログ 

