今回は2019年度山口県の平面図形の問題です。
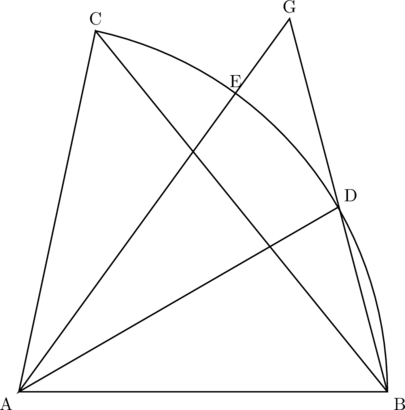
右の図のような、おうぎ形ABCがあり、![]() 上に点Dをとり、
上に点Dをとり、![]() 上に点Eを、
上に点Eを、![]() となるようにとる。また、線分AEと線分BCの交点をF、線分AEの延長と線分BDの延長の交点をGとする。
となるようにとる。また、線分AEと線分BCの交点をF、線分AEの延長と線分BDの延長の交点をGとする。
次の(1)、(2)に答えなさい。
(1) △GAD∽△GBFであることを証明しなさい。
(2) おうぎ形ABCの半径が8cm、線分EGの長さが2cmであるとき、線分AFの長さを求めなさい。

答え
(1)
△GADと△GBFで
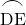 に対する円周角は等しいので、
に対する円周角は等しいので、
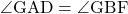 ・・・①
・・・①
共通な角なので
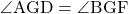 ・・・②
・・・②
①、②より2組の角がそれぞれ等しいので
△GAD∽△GBF
(2)
△ABCは二等辺三角形なので
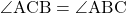 ・・・①
・・・①
また△ABDも二等辺三角形なので
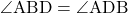
ここで
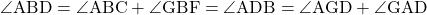 であり、
であり、
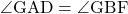 であるから
であるから
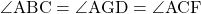
また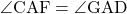 から
から
2組の角がそれぞれ等しいので
△GAD∽△CAF
よって
CA:AG AF:AD
AF:AD
8 : 10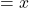 : 8
: 8
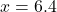
6.4cm
△GADと△GBFで
共通な角なので
①、②より2組の角がそれぞれ等しいので
△GAD∽△GBF
(2)
△ABCは二等辺三角形なので
また△ABDも二等辺三角形なので
ここで
また
2組の角がそれぞれ等しいので
△GAD∽△CAF
よって
CA:AG
8 : 10
6.4cm
 数樂管理人のブログ
数樂管理人のブログ 

