こんにちは。相城です。今回は佐賀県の文章問題からです。TeXの練習になりますかね?日本語が使えないので、TeXというより普通の文書ですね。
1日の学習時間調査を行い、40人の生徒それぞれに【選択肢】のA~Eの中から1つ選ばせた。
【選択肢】
A:4時間以上
B:3時間以上4時間未満
C:2時間以上3時間未満
D:1時間以上2時間未満
E:1時間未満
この調査の結果、2時間以上学習しているA、B、Cを選んだ生徒を合わせると、33人であることがわかった。また、Aを選んだ生徒数は5人であり、Bを選んだ生徒数の2倍からCを選んだ生徒をひくと、Aを選んだ生徒数に等しかった。
このとき、(ア)、(イ)の問いに答えなさい。
(ア) Bを選んだ生徒数を![]() 人、Cを選んだ生徒数を
人、Cを選んだ生徒数を![]() 人として、
人として、![]() 、
、![]() についての連立方程式を次のようにつくった。
についての連立方程式を次のようにつくった。
このとき![]() 、
、![]() にあてはまる式を
にあてはまる式を![]() 、
、![]() を用いてそれぞれ表しなさい。
を用いてそれぞれ表しなさい。
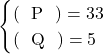
(イ) Bを選んだ生徒数と、Cを選んだ生徒数をそれぞれ求めなさい。

答え
(ア)
Aは5人、Bは 人、Cは
人、Cは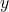 人なので
人なので
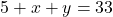
よって(P)・・・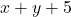
問題文より
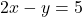
よって(Q)・・・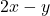
(イ)
連立方程式を解いて
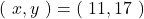
Bは11人、Cは17人
Aは5人、Bは
よって(P)・・・
問題文より
よって(Q)・・・
(イ)
連立方程式を解いて
Bは11人、Cは17人
 数樂管理人のブログ
数樂管理人のブログ 

