こんにちは。相城です。久しぶりにこういう問題解いたので苦戦したなぁという感想です。面白い問題ですので、それではどうぞ。
下の図のような、1辺12cmの正四面体OABCがあります。辺BCの中点をMとする。このとき、次の(1)、(2)の問いに答えなさい。
(1) 線分OMの長さを求めなさい。
(2) 辺OCの中点をDとし、辺OB上に線分AEと線分EDの長さの和が最も小さくなるように点Eをとる。また、線分AM上にAP : PM![]() 4 : 5となる点Pをとり、3点A、D、Eを通る平面と線分OPとの交点をQとする。
4 : 5となる点Pをとり、3点A、D、Eを通る平面と線分OPとの交点をQとする。
① 線分OMと線分DEとの交点をRとするとき、線分ORと線分RMの長さの比を求めなさい。
② 三角錐QPBCの体積を求めなさい。


答え
(1) OMは1辺12cmの正三角形の高さなので、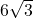 cm
cm
(2) ①
(2) ①
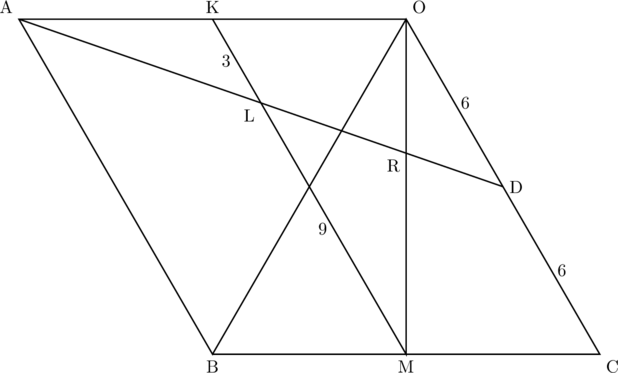
Mを通りOCに平行な線分KMを引く、KMとADの交点をLとすると、
KLは△ADOで中点連結定理より3、これからML![]() 9、またOD
9、またOD![]() 6で△ODR∽△MLRで相似比はOD : ML
6で△ODR∽△MLRで相似比はOD : ML![]() 6 : 9
6 : 9![]() 2 : 3
2 : 3![]() OR : RM。
OR : RM。
よって2 : 3・・・答え
②
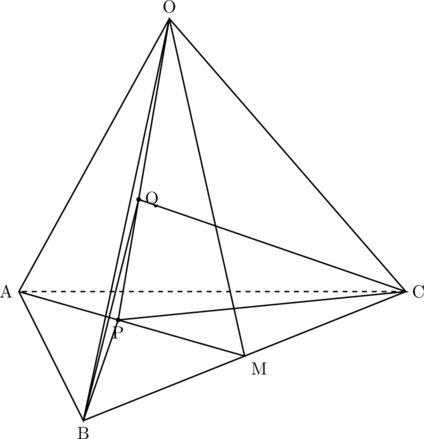
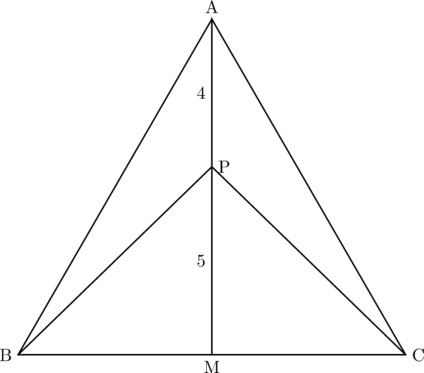
△OAMを書き出すと、
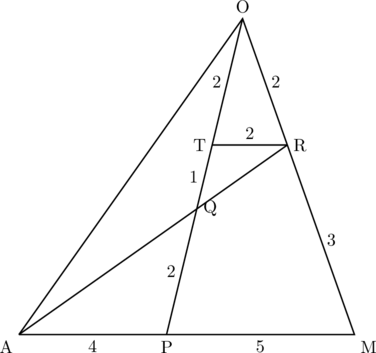
これより、OP : QP![]() 5 : 2。すなわち求める三角錐の高さは三角錐OABCの
5 : 2。すなわち求める三角錐の高さは三角錐OABCの![]() 倍・・・①。
倍・・・①。
こんどは底面の正三角形を真上から見ると、下図のようになり、三角錐QPBCの底面である△PBCは正三角形ABCの![]() 倍・・・②であることが分かる。
倍・・・②であることが分かる。
①、②より、求める体積は正四面体OABCの体積の
![]() 倍。
倍。
したがって、
三角錐QPBC
![]()
32![]() cm
cm![]() ・・・答え
・・・答え
 数樂管理人のブログ
数樂管理人のブログ 


Tikzの問題を普通にプリントアウトしたいです
他の問題のように問題だけのページも作って欲しいです!
今のところ時間的なことにより不可能です。時間に余裕ができれば考えてみます。すみませんがご理解のほどを。