整数問題・整数の性質①

こんにちは。相城です。さて整数の性質問題です。基本の確認を行っていきましょう。

問1：一の位が分からない5桁の自然数2187〇がある。これについて, 次の問いに答えよ。
(1)　この自然数が9の倍数になるとき, 〇に入る数をすべて答えよ。
(2)　この自然数が3でも4でも割り切れるとき, 〇に入る数を答えよ。

問2：5桁の自然数8〇5〇4の〇に, それぞれ0～9の10個のうち適当な数を1つずつ入れると, 3の倍数になる。このような自然数の中で最大のものを求めよ。

答え

問1
(1)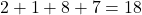 なので, 0か9　よって0, 9
(2) 3の倍数であるためには〇3, 6, 9のいずれか。
このとき, 下2桁はそれぞれ, 73, 76, 79となりこの中で4の倍数は76だけ。よって6
問2

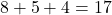
最大の数とあるので千の位に9を入れたら,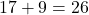
このとき26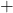〇が3の倍数になるための最も大きい数は7である。
よって〇には左から順に9, 7と入る。
したがって求める最大の自然数は89574