こんにちは。相城です。最大公約数の問題です。(3)は互除法を使ってみよう。
次の数の最大公約数を求めなさい。
(1) 60, 90
(2) 18, 48, 60
(3) 1705, 8463

答え
(1)
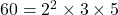
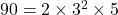 となり
となり
共通する数字は2が1個, 3も1個, 5も1個だけ共通するので,
最大公約数は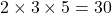
(2)
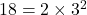
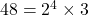
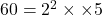 となり
となり
共通する数字は2が1個と3も1個なので,
最大公約数は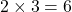
(3)
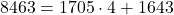
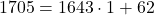
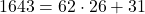
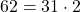
よって31
共通する数字は2が1個, 3も1個, 5も1個だけ共通するので,
最大公約数は
(2)
共通する数字は2が1個と3も1個なので,
最大公約数は
(3)
よって31
 数樂管理人のブログ
数樂管理人のブログ 

