2020年2月に徳島県で行われました、中1生対象の基礎学力テストより扇形の問題をピックアップ。回転系の問題では有名問題ですのでやっておきましょう。少し古臭い問題ではありますが。中学受験などではよく扱う問題だと思います。
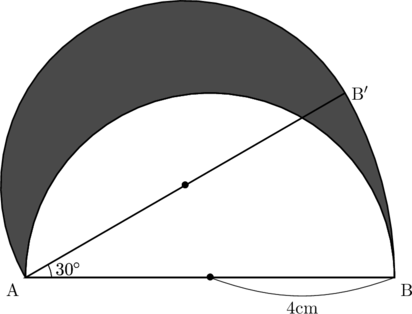
下の図は、半径4cmの半円を点Aを回転の中心として時計の針の回転と反対の向きに30![]() 回転移動したものである。この移動によって、点Bは点B
回転移動したものである。この移動によって、点Bは点B![]() に移っている。このとき、下の図の影をつけた部分の面積を求めなさい。ただし、円周率は
に移っている。このとき、下の図の影をつけた部分の面積を求めなさい。ただし、円周率は![]() とします。
とします。

答え
求める面積は半径8cm、中心角30 の扇形の面積と同じになる。
の扇形の面積と同じになる。
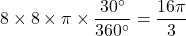
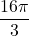 cm
cm
【理由】
求める面積は扇形ABB (P)と直径がAB
(P)と直径がAB の半円(Q)を足したものから直径をABとする半円(R)を引いたものである。
の半円(Q)を足したものから直径をABとする半円(R)を引いたものである。
つまり、P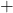 Q-Rであるが、QとRは同じ図形(合同)であるから、打ち消し合う。よって、P
Q-Rであるが、QとRは同じ図形(合同)であるから、打ち消し合う。よって、P Q-R=P
Q-R=P
【理由】
求める面積は扇形ABB
つまり、P
 数樂管理人のブログ
数樂管理人のブログ 

