こんにちは。相城です。2020年2月に徳島県で行われた中2の基礎学力テストの問題から平面図形の問題をお届けします。それではどうぞ。
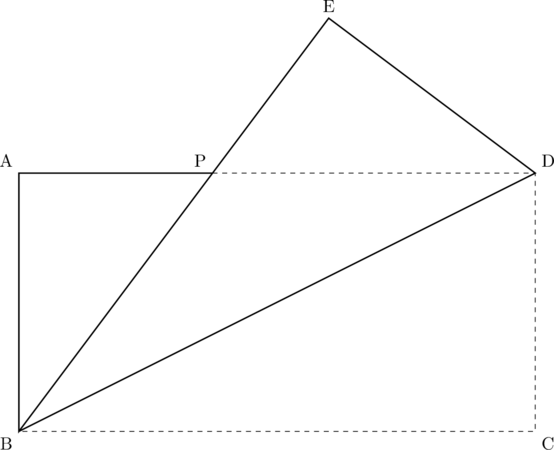
下の図は、長方形ABCDを対角線BDを折り目として折り返したものである。ADとBEの交点を点Pとするとき、次の(1)~(3)に答えなさい。
(1) ![]() のとき、
のとき、![]() の大きさを求めなさい。
の大きさを求めなさい。
(2) △ABP![]() △EDPであることを証明しなさい。
△EDPであることを証明しなさい。
(3) AP![]() 6cm、PB
6cm、PB![]() 10cmのとき、△APBの面積は長方形ABCDの面積の何倍になるか求めなさい。
10cmのとき、△APBの面積は長方形ABCDの面積の何倍になるか求めなさい。

答え
(1) 25
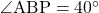 より、
より、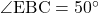 。
。
△EBD≡△CBDより、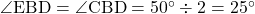 。AD//BCより錯角は等しいので、
。AD//BCより錯角は等しいので、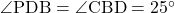
(2)
△ABPと△EDPで
仮定より、
AB ED・・・①
ED・・・①
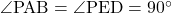 ・・・②
・・・②
対頂角は等しいので、
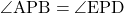 ・・・③
・・・③
②、③と三角形の内角の関係により
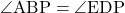 ・・・④
・・・④
①、②、④より、
1組の辺とその両端の角がそれぞれ等しいので
△ABP △EDP
△EDP
※△PBDが二等辺三角形であることを示し、PB PDを示し、直角三角形の斜辺と他の一辺がそれぞれ等しいでも可。
PDを示し、直角三角形の斜辺と他の一辺がそれぞれ等しいでも可。
(3)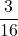 倍
倍
△APBは△ABDの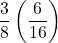 倍である。また、△ABDは長方形ABCDの
倍である。また、△ABDは長方形ABCDの 倍であるから、長方形の面積を
倍であるから、長方形の面積を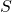 とすると、
とすると、
△APB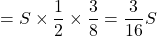
よって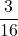 倍
倍
【アドバンスド】三角形を上底が0の台形とし、長方形を上底と下底が等しい台形とみると、△APBと長方形ABCDは高さが等しいので面積比は(上底+下底)の比になる。
よって、△APB : 長方形ABCD (0
(0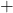 6) : (16
6) : (16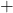 16)
16) 3 : 16
3 : 16
したがって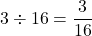 倍
倍
△EBD≡△CBDより、
(2)
△ABPと△EDPで
仮定より、
AB
対頂角は等しいので、
②、③と三角形の内角の関係により
①、②、④より、
1組の辺とその両端の角がそれぞれ等しいので
△ABP
※△PBDが二等辺三角形であることを示し、PB
(3)
△APBは△ABDの
△APB
よって
【アドバンスド】三角形を上底が0の台形とし、長方形を上底と下底が等しい台形とみると、△APBと長方形ABCDは高さが等しいので面積比は(上底+下底)の比になる。
よって、△APB : 長方形ABCD
したがって
 数樂管理人のブログ
数樂管理人のブログ 

