こんにちは。相城です。2020年の2月28日に埼玉県で行われた高校入試問題より。それではどうぞ。
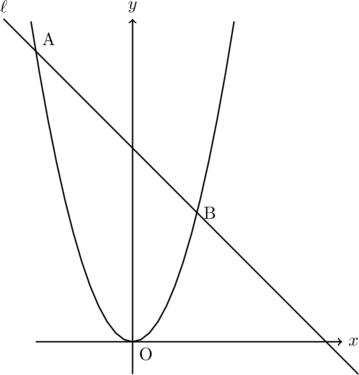
図1において、曲線は![]() のグラフで。直線
のグラフで。直線![]() は点A(
は点A(![]() )、点B(
)、点B(![]() )で曲線と交わっています。
)で曲線と交わっています。
このとき、次の各問いに答えなさい。
(1) 直線![]() の式を求めなさい。
の式を求めなさい。
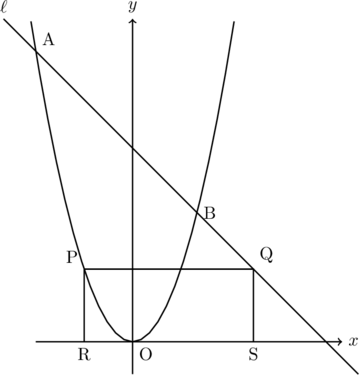
(2) 下の図2において、曲線上を点Aから点Bまで動く点Pをとり、点Pから![]() 軸と平行な直線をひき、直線
軸と平行な直線をひき、直線![]() との交点をQとします。また、点P、Qから
との交点をQとします。また、点P、Qから![]() 軸へ垂線をひき、
軸へ垂線をひき、![]() 軸との交点をそれぞれR、Sとします。
軸との交点をそれぞれR、Sとします。
このとき、次の①、②に答えなさい。
① 長方形PRSQが正方形になる点Pの座標を、途中の説明も書いてすべて求めなさい。その際。「点Pの![]() 座標を
座標を![]() とおくと、」に続けて説明しなさい。
とおくと、」に続けて説明しなさい。
② △BPQと△OPQの面積比が1 : 3となる点Qの座標を、すべて求めなさい。

答え
(1) 2点(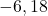 )、(
)、(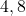 )を通る直線の式は
)を通る直線の式は
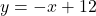
(2)
点Pの 座標を
座標を とおくと、P
とおくと、P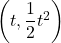
Qの 座標はPの
座標はPの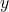 座標と同じなので、
座標と同じなので、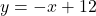 で
で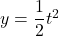 とおくと、
とおくと、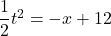 となり、
となり、 について解くと、
について解くと、
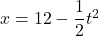 となる。よってQの座標はQ
となる。よってQの座標はQ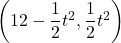 。
。
長方形PRSQが正方形になるということは、縦と横の長さが等しくなる。
PR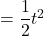 、PQ
、PQ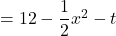
PR PQとして方程式をつくって解くと、
PQとして方程式をつくって解くと、
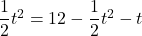
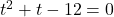
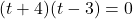
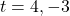
よってP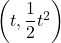 より、
より、
(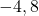 )、
)、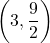
(3)
△BPQと△OPQではPQが共通なので、これを底辺と考えると、面積の比は高さの比と同じになる(高さの比に比例する)。
Qの位置で2通りに場合分けする。点Pの 座標を
座標を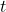 とし、①で用いた
とし、①で用いた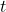 で表した座標をそのまま用いるとする。
で表した座標をそのまま用いるとする。
まず、下図のQがBより下にある場合。
(2)
点Pの
Qの
長方形PRSQが正方形になるということは、縦と横の長さが等しくなる。
PR
PR
よってP
(
(3)
△BPQと△OPQではPQが共通なので、これを底辺と考えると、面積の比は高さの比と同じになる(高さの比に比例する)。
Qの位置で2通りに場合分けする。点Pの
まず、下図のQがBより下にある場合。
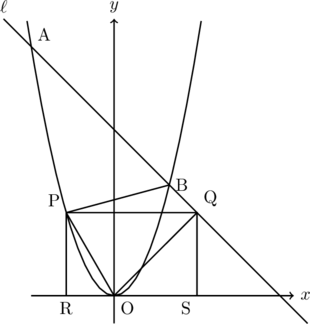
△BPQの高さは![]() 、△OPQの高さは
、△OPQの高さは![]()
これが1 : 3なので、
![]()
![]()
![]()
![]()
このとき、Q(6, 6)。
次は下図のとき、QがBより上にある場合。
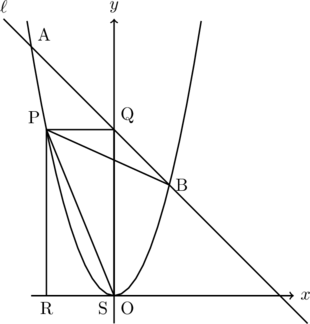
△BPQの高さは![]() 、△OPQの高さは
、△OPQの高さは![]()
これが1 : 3なので、
![]()
![]()
![]()
![]()
このとき、Q(0, 12)。
以上より求めるQの座標は、(6, 6)、(0, 12)
 数樂管理人のブログ
数樂管理人のブログ 

