こんにちは。相城です。今回は球の体積の何で?にお答えできればと存じます。
球の体積の公式のなぜ?
球の中心を![]() とし, 頂点を
とし, 頂点を![]() とする正四角錐で球を
とする正四角錐で球を![]() 等分していくことを考える。
等分していくことを考える。
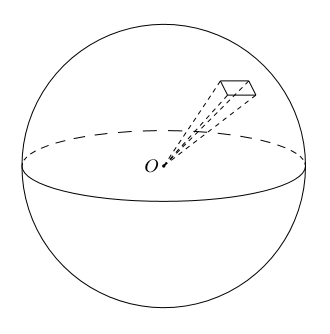
このとき, ![]() を無限に近づけていくと, 四角錐の高さは球の半径
を無限に近づけていくと, 四角錐の高さは球の半径![]() に限りなく等しくなる。また, 球の表面積は
に限りなく等しくなる。また, 球の表面積は![]() 等分される。このとき
等分される。このとき![]() 等分された面積を
等分された面積を![]() とすると,
とすると, ![]() を底面とする正四角錐の1つ分の体積は
を底面とする正四角錐の1つ分の体積は
![]()
で求められる。
これを
球の体積
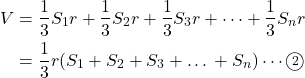
となる。
ここで
![]()
整理して
![]()
別解
![]() からの別解
からの別解![]() 等分した正四角錐1つ分の体積
等分した正四角錐1つ分の体積![]() は
は![]() より,
より,
![]()
これが
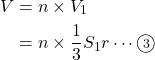
ここで
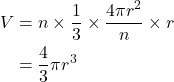
よって,
球の体積
![]()
 中学数学:球の表面積のなぜ?
中学数学:球の表面積のなぜ? 数樂管理人のブログ
数樂管理人のブログ 

