中学数学：攻略・関数と図形(四角形)

こんにちは。相城です。今回は関数と図形の四角形の捉え方を見ていきましょう。それではどうぞ。

座標軸上の四角形の面積を求めるのは, 大別して3通りある。

解法1

等積変形を行って, 四角形を三角形に変換して求める。用途低め
考え方
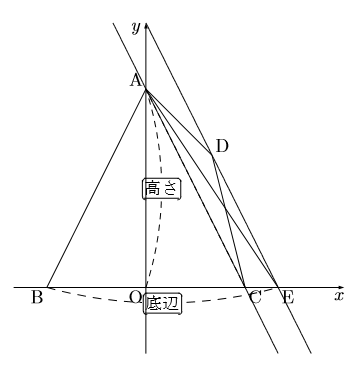
図のように対角線で三角形2つに分けて, 片方の三角形の頂点を平行移動させ,
もとの四角形ABCDと等しい面積の△ABEを作り求める。この方法はあまり使わないが, たまに応用問題で使うことがあるので押さえておきたい。図の場合では対角線ACの式の傾きを求め, その傾きを持つ直線(ACに平行な直線)が, 点Dを通る場合を考える。その直線と $x$ 軸の交点をEとし, △ADCの頂点Dを点Eへ移動させ, △ADC $=$ △AECとできる。
よって, 四角形ABCD $=$ △ABEとなる。

解法2

三角形2つに分けて、それぞれの面積の和として四角形の面積を求める方法。用途高め
考え方
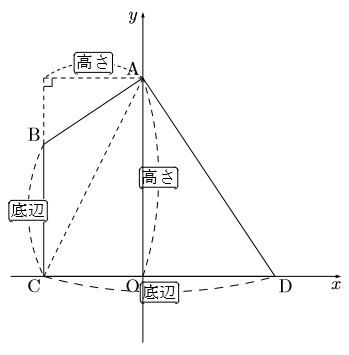
三角形2つに分けて, それぞれの面積を直接求める。図の場合だと,
四角形ABCD $=$ △ABC $+$ △ACD
このパターンの場合, 三角形を等積変形せずとも両方の三角形が簡単に求まるのがほとんどである。

解法3

大きい三角形 $-$ 小さい三角形。解法2を使う人は用途が低いかも。用途中くらい。
考え方
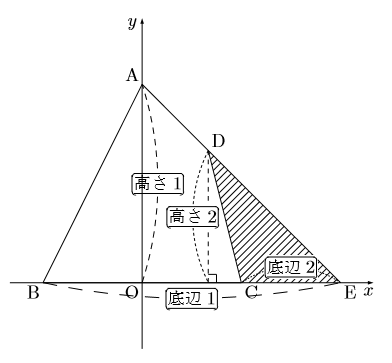
図のように, 大きい三角形から余分な三角形を取り除いて求める。等積変形など
難しい知識がなくても解ける場合があるので, 知っておくと便利。図では四角形ABCD を求めるのに, △ABEから△DCEを引いて求めています。使う公式も三角形の面積の公式で事足りるので, 抑えておきましょう。