こんにちは。相城です。さて, 今回は関数と線分の長さの攻略法というか, 一つの解き方の提案をいたします。今まであった解き方かもしれませんが, この解法での解説を今まで拝見したことがなかったので, 提案としました。それではどうぞ。
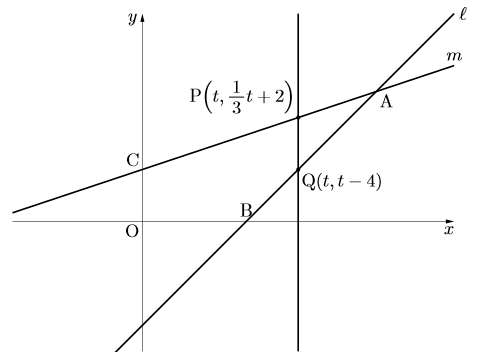
右の図で, 直線![]() は関数
は関数![]() のグラフであり, 直線
のグラフであり, 直線![]() は関数
は関数![]() のグラフである。 点Aは直線
のグラフである。 点Aは直線![]() と
と![]() との交点で, 点Bは直線
との交点で, 点Bは直線![]() と
と![]() 軸との交点, 点Cは直線
軸との交点, 点Cは直線![]() と
と![]() 軸との交点である。線分AC上に点A, Cと異なる点Pをとり, 点Pを通り
軸との交点である。線分AC上に点A, Cと異なる点Pをとり, 点Pを通り![]() 軸に平行な直線を引き, 直線
軸に平行な直線を引き, 直線![]() との交点をQとする。 PQ
との交点をQとする。 PQ![]() 2となるときの点Pの座標を求めなさい。
2となるときの点Pの座標を求めなさい。
この問題の代表的な(個人の感想です。)を示したいと思います。
求めたいPの座標を文字を使って表します。Pの![]() 座標を
座標を![]() と置くと, P
と置くと, P![]() となり, PQ
となり, PQ![]()
![]() 軸 だから, Qの
軸 だから, Qの![]() 座標も
座標も![]() なので, Qを
なので, Qを![]() を用いて表すと, Q(
を用いて表すと, Q(![]() ,
, ![]() )となります。
)となります。
ここで,
![]() (
(![]() の
の![]() 座標)-(
座標)-(![]() の
の![]() 座標)
座標)
で, PQ![]() 2であるから, 次の方程式ができます。
2であるから, 次の方程式ができます。
![]()
これを解いて,
したがって, 求めるPの座標は, P(6, 4)
次はこれとは違った, 図形の性質を使って求めてみたいと思います。座標を文字で置くことはございません。以下ににそれを書きました。
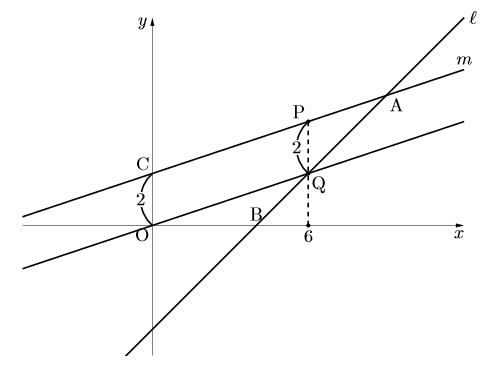
【方針】四角形COQPが平行四辺形になるこを用いて解くことにします。
したがって, 点Cから下に2(PQ![]() 2より)進んだ原点Oを通り, 直線
2より)進んだ原点Oを通り, 直線![]() に平行な直線
に平行な直線![]() と
と![]() の交点がQになり, Qの
の交点がQになり, Qの![]() 座標とPの
座標とPの![]() 座標が等しいことからPの座標を求めるという解法でやってみます。
座標が等しいことからPの座標を求めるという解法でやってみます。
【方針】より, 原点Oを通り![]() に平行な直線は
に平行な直線は![]() で, これと
で, これと![]() の交点Qの
の交点Qの![]() 座標を 求めるために方程式をつくると,
座標を 求めるために方程式をつくると,
![]()
これを解いて,
![]()
よって, Pの座標は, P(6, 4)
【別解】Qを求めると, Q(6, 2)でPはQより上に2進んだところなので, P(6, 4)としてもよい。
この解法は, 今回だけの特殊な場合ではなさそうですね。PQ![]() 5なら点Cから下に5進んだ点を通り, 直線
5なら点Cから下に5進んだ点を通り, 直線![]() に平行な直線を 考えることで, 同様にできることがわかるでしょう。ではでは。
に平行な直線を 考えることで, 同様にできることがわかるでしょう。ではでは。
 数樂管理人のブログ
数樂管理人のブログ 

