こんにちは。相城です。今回は平方根のところに登場する整数部, 小数部のお話ですが, 公立高校の入試では見かけたことはあまりない気がします。むしろ高校生の数学で登場してくることが多いかもしれません。とにかく極端に困難ではないと思いますので, やってみましょう。
根号のもつ数字の整数部分, 小数部分のとらえ方以下のような数直線をイメージできれば問題ないと思います。
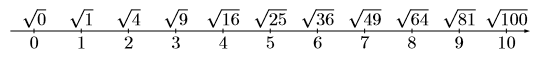
【例1】![]() の整数部分, 小数部分はいくつですか。
の整数部分, 小数部分はいくつですか。
上の数直線から, ![]() は
は![]() (
(![]() 2)と,
2)と, ![]() (
(![]() 3)の間にある数字なので, 少数で表すと,
3)の間にある数字なので, 少数で表すと, ![]() となるので, 整数部分は2となります。また, このことより
となるので, 整数部分は2となります。また, このことより![]() の 小数部分は
の 小数部分は![]() から整数部分2を引いた
から整数部分2を引いた![]() となります。
となります。
慣れてくると, ![]() から,
から, ![]() と出せるようになります。
と出せるようになります。
このように考えて次の例を考えてみましょう。
【例2】 ![]() の整数部分, 小数部分はいくつですか。
の整数部分, 小数部分はいくつですか。
![]() だから,
だから, ![]() より,
より, ![]() だから, 整数部分は7, 小数部分は
だから, 整数部分は7, 小数部分は![]() となります。
となります。
最後にこれ
【例3】 ![]() の整数部分, 小数部分はいくつですか。
の整数部分, 小数部分はいくつですか。
この考え方も同じように考えることが可能です。
![]() より,
より, ![]() より, 整数部分は5, となるので, ①は
より, 整数部分は5, となるので, ①は![]() となるので, 整数部分は3。これより, ①の小数部分は①から3を引けばよいので, 小数部分は
となるので, 整数部分は3。これより, ①の小数部分は①から3を引けばよいので, 小数部分は![]() となります。
となります。
これに関しては, 小数部分は結局![]() の小数部分を考えているにすぎないので,
の小数部分を考えているにすぎないので, ![]() を 無視してとらえても何んら問題ないと思います。
を 無視してとらえても何んら問題ないと思います。
ではでは。
ポイント
イメージしにくいときは数直線を![]() で表して考えるとよい。
で表して考えるとよい。
 数樂管理人のブログ
数樂管理人のブログ 

