こんにちは。今回は階差数列の規則性についてです。階差数列にはあまり触れませんので気軽に読んでください。
規則性の攻略(差の差が一定の場合・階差数列)
〇 数字の差を調べたが差が等しくない場合がある。ただその差の数字を見たとき, 一定の差があるときは掛け算に直すと片付く問題が多い。
〇 1で掛け算に直すと片付くとあるが, 数え方の工夫をすれば難しいことはしなくても片付くことが多い。
I図のように同じ大きさの白色のタイルがある。これをII図のようにある規則に従って, 隙間なく並べていく。![]() 番目に使う白色のタイルの総数を
番目に使う白色のタイルの総数を![]() を使って表しなさい。この例を使って考えてみる。
を使って表しなさい。この例を使って考えてみる。
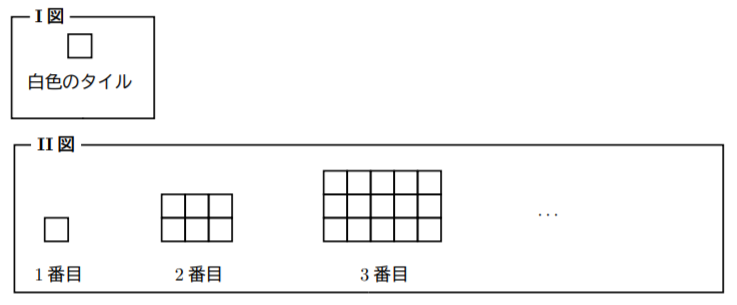
もし仮に勢い余ってタイルを数えたとする。4番目まで図形を書いて調べたとすると
1, 6, 15, 28, ![]()
となる。差を調べてみると,
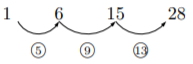
となり差が5, 9, 13, ![]() で一定ではない。ただ, 差の5, 9, 13,
で一定ではない。ただ, 差の5, 9, 13, ![]() をみると,
をみると,
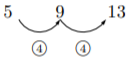
で差が4で一定である。この場合, 1, 6, 15, 28, ![]() の数字から掛け算に直す(
の数字から掛け算に直す(![]() 番目の式を得る)こともできるが, 差が一定でない場合は, 数え方の工夫でその掛け算の式を導くことができる。
番目の式を得る)こともできるが, 差が一定でない場合は, 数え方の工夫でその掛け算の式を導くことができる。
この場合できる図形が長方形なので, 縦![]() 横でタイルの総数は求まる。
横でタイルの総数は求まる。
1番目は1![]() 1(枚),
1(枚),
2番目は2![]() 3(枚),
3(枚),
3番目は3![]() 5(枚),
5(枚),
4番目は4![]() 7(枚),
7(枚),
のようになり, ![]() 番目は
番目は![]() (枚)
(枚)
となり, ![]() (枚)となる。
(枚)となる。
差が一定でなくとも, その差の差を調べて一定なら, 数え方を工夫する方法を考えたほうが良い。
特によく出てくる数字は, 1, 4, 9, 16, 25, ![]() であって,
であって, ![]() 番目の数字は
番目の数字は![]() という具合なのでこれは抑えておきたい。
という具合なのでこれは抑えておきたい。
 数樂管理人のブログ
数樂管理人のブログ 

