高校数学：二重根号のお話

こんにちは。相城です。今回は二重根号について書いていきます。

二重根号のなぜ

例えば, 二重根号 $\sqrt{5+2\sqrt{6}}$ をはずしなさい。
とあった場合, 答えはなぜ $\sqrt{3}+\sqrt{2}$ になるのでしょうか。
逆を考えながら説明してみましょう。
逆というのは,
$\sqrt{3}+\sqrt{2}$ を二重根号で表わしてみましょう。
つまり, こうです。

$\begin{align*}\sqrt{3}+\sqrt{2}&=\sqrt{(\sqrt{3}+\sqrt{2})^2}\\&=\sqrt{3+2\sqrt{3\times2}+2}\\&=\sqrt{3+2+2\sqrt{3\times2}}\cdots\textcircled{\scriptsize1}\\&=\sqrt{5+2\sqrt{6}}\cdots\textcircled{\scriptsize2}\end{align*}$

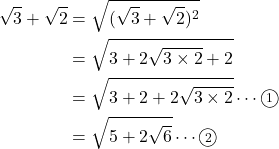
ここでポイントなのは $\textcircled{\scriptsize1}$ と問題の $\textcircled{\scriptsize2}$ の関係です。
5はある2数(ここでは3と2)の和で構成され $2\sqrt{6}$ の2は2倍を意味し, $\sqrt{\hspace{3mm}}$ 中の6はある2数(ここでは3と2)の積で与えられます。
つまり, $5+2\sqrt{6}$ は $\sqrt{3}+\sqrt{2}$ の平方(2乗)で得られることが分かります。したがって,

$\begin{align*}\sqrt{5+2\sqrt{6}}&=\sqrt{(\sqrt{3}+\sqrt{2})^2}\\&=\sqrt{3}+\sqrt{2}\end{align*}$

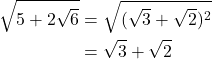
となります。
ちなみに, 引き算の場合の二重根号の方が間違えやすく,
$\sqrt{\mathstrut5-2\sqrt{6}}=\sqrt{\mathstrut\left(\sqrt{2}-\sqrt{3}\right)^2}=\sqrt{2}-\sqrt{3}$
ではありません。これでは $\sqrt{2}-\sqrt{3}<0$ となってしまうので, 話がおかしくなります。
この場合, 正しくは
$\sqrt{\mathstrut5-2\sqrt{6}}=\sqrt{\mathstrut\left(\sqrt{3}-\sqrt{2}\right)^2}=\sqrt{3}-\sqrt{2}$
となります。根号の中は正の数でなくてはなりませんからね。気を付けていきましょう。
これらを一般化すると以下の公式が得られます。
これを用いた二重根号の外し方はこちらをご覧ください。

二重根号の公式

$a>0, b>0$
$\sqrt{\mathstrut(a+b)+2\sqrt{ab}}=\sqrt{\mathstrut a}+\sqrt{\mathstrut b}$
$\sqrt{\mathstrut(a+b)-2\sqrt{ab}}=\sqrt{\mathstrut a}-\sqrt{\mathstrut b}\ (a>b)$

プリントアウト用pdf

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル