こんにちは。相城です。今回は排反と和事象の確率について書いておきます。
排反と独立
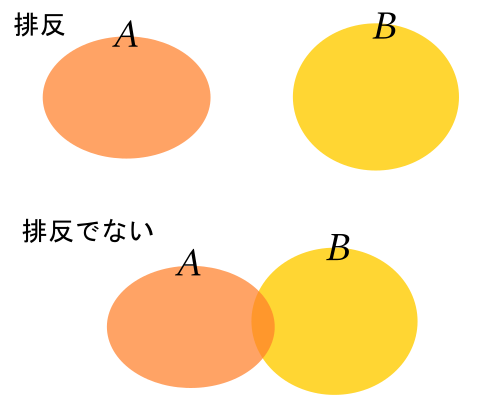
排反とはお互いに同時に起こらないことを指して言います。
例えば, 袋の中に赤, 白, 青の玉が1個ずつ入っていて, そこから玉を1個取り出すとき, 赤玉を取り出すことと, 青玉を取り出すことは同時に起こらないですよね。こういった事象を, 排反と言います。
独立とは, お互いに影響を与えないことを独立と言います。この場合だと玉を1個取り出すという試行は独立しているといいます。
つまり, 事象に使う言葉が排反で, 試行に使う言葉が独立だと認識していいでしょう。
排反事象の確率
排反事象の確率の計算
2つの事象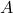 と事象
と事象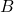 が互いに排反であるとき,
が互いに排反であるとき, 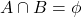
事象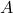 の起こる確率を
の起こる確率を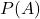 , 事象
, 事象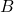 が起こる確率を
が起こる確率を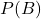 とするとき,
とするとき,
事象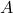 または, 事象
または, 事象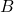 が起こる確率は,
が起こる確率は,
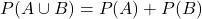
で求められます。
このことは, 3つ以上の事象でも成り立ちます。
事象
事象
で求められます。
このことは, 3つ以上の事象でも成り立ちます。

例題を見てみよう
【例題】袋Aには赤玉4個, 青玉3個, 袋Bには赤玉3個, 青玉2個がそれぞれ入っている。この袋から1個ずつ玉を取り出すとき, 同じ色の玉を取り出す確率を求めよ。
【解法】同じ色の玉を取り出すということは, 赤で同じのときと, 青で同じの2通りを考える。この2つの事象は互いに排反であるから, 求める確率![]() は,
は, ![]() =(2個とも赤である確率)+(2個とも青である確率)
=(2個とも赤である確率)+(2個とも青である確率)
玉を取り出すという試行は独立であるため,
①袋Aから赤玉を取り, 袋Bからも赤玉を取り出す確率は, ![]()
②袋Aから青玉を取り, 袋Bからも青玉を取りだす確率は, ![]()
①, ②の事象は互いに排反であるので, 求める確率![]() は
は![]()
 数樂管理人のブログ
数樂管理人のブログ 

