こんにちは。相城です。今回は球の表面積について書いていこうと思います。
中学生でも納得かな?なぜ球の表面積は![]() なのかを証明しよう。
なのかを証明しよう。
先ず半径![]() , 中心角
, 中心角![]() の扇形から, 半径
の扇形から, 半径![]() , 中心角
, 中心角![]() の扇形を引いた面積
の扇形を引いた面積![]() は次の式で表される。
は次の式で表される。![]()
ただし![]() は幅
は幅![]() の部分の中央線である。
の部分の中央線である。
証明
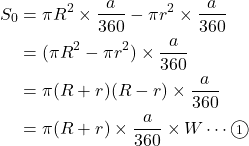
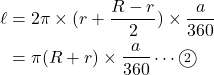
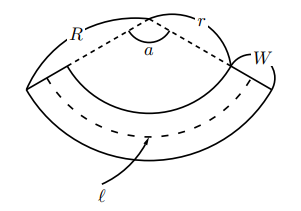
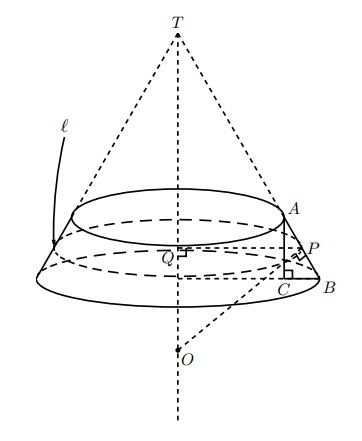
このような考え方を使って, 直円錐の側面積の一部分を考える。先の扇形と同じように半径![]() の扇形から, 半径
の扇形から, 半径![]() の扇形を引いた面積
の扇形を引いた面積![]() は次の式で与えられる。
は次の式で与えられる。![]()
ただし、![]() は幅
は幅![]() の部分の中央線である。
の部分の中央線である。
![]() は
は![]() の中点で
の中点で![]() 上にあり,
上にあり, ![]() から直円錐の高さに下ろした垂線と高さの交点を
から直円錐の高さに下ろした垂線と高さの交点を![]() とし,
とし, ![]() を通り
を通り![]() に垂直な線と高さの延長線との交点を
に垂直な線と高さの延長線との交点を![]() とすると,
とすると, ![]() であるから,
であるから, ![]() 式は
式は![]()
また△ACB∽△PQOであるから, ![]()
これより, ![]()
![]() は
は![]() より,
より, ![]()
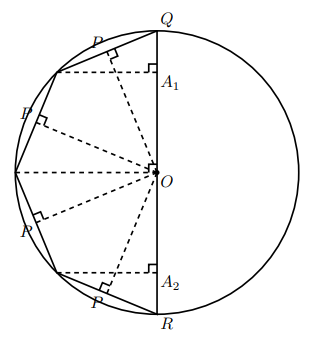
球を直径![]() の半円を1回転させてできる立体と考える。その半円を図のように4等分して頂点を結ぶと, ちょうど正八角形の半分ができる。
の半円を1回転させてできる立体と考える。その半円を図のように4等分して頂点を結ぶと, ちょうど正八角形の半分ができる。
これを![]() を軸として回転させてできる立体の表面積
を軸として回転させてできる立体の表面積![]() を考えるとき, 先の
を考えるとき, 先の![]() の式を使って,
の式を使って,
次のように与えられる。![]()
![]()
![]()
上の![]() 式は, 4等分での結果の式であるが, これを
式は, 4等分での結果の式であるが, これを![]() 等分にしても同じ結果が得られるのは気づいていただけたでしょうか。
等分にしても同じ結果が得られるのは気づいていただけたでしょうか。
従って![]() 等分した時の面積
等分した時の面積![]() は同様に
は同様に![]()
この![]() を無限に近づけていくと,
を無限に近づけていくと, ![]() は
は![]() の半分すなわち半径に等しくなる。この半円の半径を
の半分すなわち半径に等しくなる。この半円の半径を![]() とすると,
とすると, ![]() となり,
となり,
これを![]() に代入すると,
に代入すると,
![]()
となる。従って半径
 中学数学:球の体積の何で?
中学数学:球の体積の何で? 数樂管理人のブログ
数樂管理人のブログ 


証明も書いているので、分かりやすいので、僕的には、良かったです。これからもよろしくお願いします。
こちらこそありがとうございます。
引き続き楽しんでください。