こんにちは。相城です。今回は3項間の漸化式について書いておきます。
3項間漸化式の解法の大まかな流れ
漸化式![]() について,
について, ![]() は次のようにして求めることができる。漸化式の
は次のようにして求めることができる。漸化式の![]() ,
, ![]() ,
, ![]() をそれぞれ,
をそれぞれ, ![]() ,
, ![]() ,
, ![]() で置き換えた特性方程式
で置き換えた特性方程式![]() の解を
の解を![]() ,
, ![]() とする。
とする。
このとき, ![]() は
は![]() と同値なので,
と同値なので, ![]()
![]() ,
, ![]() ,
, ![]() をそれぞれ
をそれぞれ![]() ,
, ![]() ,
, ![]() で置き換えると
で置き換えると![]()
展開すると, ![]()
左辺に![]() を残して, 残りを右辺に移項して
を残して, 残りを右辺に移項して![]() でくくると,
でくくると, ![]()
同様に, 左辺に![]() を残して, 残りを右辺に移項して
を残して, 残りを右辺に移項して![]() でくくると,
でくくると,![]()
この![]() を用いて一般項
を用いて一般項![]() を求めることになる。
を求めることになる。
以下に特性方程式の解![]() が
が![]() (異なる2つの解),
(異なる2つの解), ![]() (重解),
(重解), ![]() ,
, ![]() の一方が1になる場合について例題と解き方を書いておきます。
の一方が1になる場合について例題と解き方を書いておきます。
異なる2つの解(α≠βのとき)
【例題】次の条件によって定められる数列![]() の一般項
の一般項![]() を求めなさい。
を求めなさい。![]()
【解法】特性方程式![]() とすると,
とすると, ![]() なので,
なので, ![]() として, 漸化式を変形すると,
として, 漸化式を変形すると, ![]()
![]()
![]() より, 数列
より, 数列![]() は初項
は初項![]() , 公比3の等比数列である。したがって,
, 公比3の等比数列である。したがって, ![]()
また, 同様に, ![]() より, 数列
より, 数列![]() は初項
は初項![]() , 公比2の等比数列である。したがって,
, 公比2の等比数列である。したがって,![]()
![]() で,
で, ![]() を消去して,
を消去して, ![]() を求めると,
を求めると, ![]() (答)
(答)
と変形する。
変形した2つの式から, それぞれ数列を求める。
重解のとき(α=βのとき)
【例題】次の条件によって定められる数列![]() の一般項
の一般項![]() を求めなさい。
を求めなさい。![]()
【解法】特性方程式![]() とすると,
とすると, ![]() となり,
となり, ![]() として, 漸化式を変形すると,
として, 漸化式を変形すると, ![]()
![]() は, 初項
は, 初項![]() , 公比
, 公比![]() の等比数列である。したがって,
の等比数列である。したがって, ![]()
ここで, 両辺を![]() で割ると,
で割ると, ![]()
![]()
![]()
よって, 数列![]() は, 初項
は, 初項![]() , 公差
, 公差![]() の等差数列である。したがって,
の等差数列である。したがって, ![]()
![]()
![]() (答)
(答)
と変形する。
変形した式から,
以下の等差数列の形に持ち込み解く。
解に1を含むとき(αかβが1のとき)
【例題】次の条件によって定められる数列![]() の一般項
の一般項![]() を求めなさい。
を求めなさい。![]()
【解法】特性方程式![]() とすると,
とすると, ![]() なので,
なので, ![]() として, 漸化式を変形すると,
として, 漸化式を変形すると, ![]()
![]()
より, 1を略して書くと, ![]()
![]()
![]() より,
より,
数列![]() は, 初項
は, 初項![]() , 公比
, 公比![]() の等比数列である。したがって,
の等比数列である。したがって, ![]()
これは, 2項間の階差数列が等比数列になることを表している。
したがって, 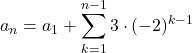
![]()
![]()
と変形する。
変形した式から,
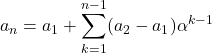
 数樂管理人のブログ
数樂管理人のブログ 

