こんにちは。今回は確率の最大値に触れておきたいと思います。早速ですが, 例題を見ていきましょう。
つぼの中に![]() 個の白い玉がある。このつぼから5つの玉を取り出し赤印をつけてもとに戻す。よくかきまぜてから今度は2個の玉を取り出すとき, 赤印をつけたものが1個だけである確率
個の白い玉がある。このつぼから5つの玉を取り出し赤印をつけてもとに戻す。よくかきまぜてから今度は2個の玉を取り出すとき, 赤印をつけたものが1個だけである確率![]() は【 ① 】である。また, この確率を最大にする
は【 ① 】である。また, この確率を最大にする![]() の値を求めると, 【 ② 】と【 ③ 】である。
の値を求めると, 【 ② 】と【 ③ 】である。
【解法】
前置きはいいとして, つまり, 5個の赤玉と![]() 個の白玉があるということになる。
個の白玉があるということになる。
すべての玉の取り出し方は, ![]() で, 取り出すのは1個が赤玉, 1個が白玉なので, 起こりうる場合の数は,
で, 取り出すのは1個が赤玉, 1個が白玉なので, 起こりうる場合の数は, ![]() である。したがって, 求める確率
である。したがって, 求める確率![]() は,
は, 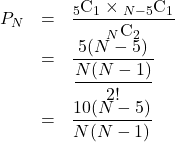
![]() の(答)
の(答)
続いて, これを用いて![]() を
を![]() を使って表し,
を使って表し, ![]() の商を考えることにする。
の商を考えることにする。![]() なら
なら![]() ということで,
ということで, ![]() なら
なら![]() ,
, ![]() なら
なら![]() ということになります。
ということになります。
この結果から, ![]() の最大値を求めることにします。
の最大値を求めることにします。![]() は
は![]() の結果において,
の結果において, ![]() を
を![]() に置き換えたものだから,
に置き換えたものだから, 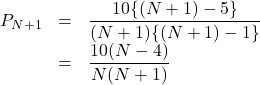
したがって, ![]() は,
は, 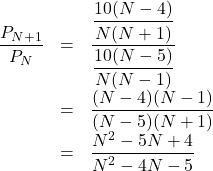
( i ) ![]() のとき,
のとき, ![]()
![]()
![]() (以下方程式の途中式割愛)となり,
(以下方程式の途中式割愛)となり, ![]() が9より小さいときは
が9より小さいときは![]()
例えば![]() なら,
なら, ![]() となる。
となる。
( ii ) ![]() のとき,
のとき,![]() となり,
となり, ![]() となる。
となる。
(iii) ![]() のとき,
のとき,![]() となり,
となり, ![]() が9より大きいときは,
が9より大きいときは, ![]()
例えば![]() なら,
なら, ![]() となる。
となる。
( i ), ( ii ), (iii)より![]()
よって![]() が最大になる
が最大になる![]() は
は![]() の答え(順不同)
の答え(順不同)
テクニック
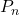 を求めるのに, 次の公式をよく用います。
を求めるのに, 次の公式をよく用います。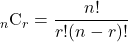
例えば,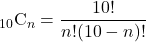
となります。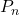 を求めた後,
を求めた後, 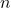 を
を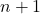 に置き換えて,
に置き換えて, 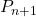 を求める。
を求める。
そして,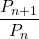 を計算する。
を計算する。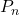 が最大になる
が最大になる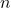 は以下から判断する。
は以下から判断する。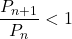
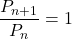
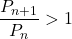
 数樂管理人のブログ
数樂管理人のブログ 

