高校数学：確率と漸化式

こんにちは。今回は確率と漸化式です。有名な？例題をやってみようと思います。

例題を見てみよう

A君は日記をなるべくつけるようにした。日記をつけた日の翌日は確率 $\dfrac23$ で日記をつけ，日記をつけなかった日の翌日は確率 $\dfrac56$ で日記をつけているという。初日に日記をつけたとして，第 $n$ 日に日記をつける確率を $p_n$ とする。このとき, 次の問いに答えよ。(日大改)
(1) $p_{n+1}$ を $p_n$ を用いて表せ。
(2) $p_n$ を求めよ。

解法

【解法】
(1) $p_{n+1}$ を考える場合, つまり, ( $n+1$ )日目に日記をつける場合は, $n$ 日目にどういう状況か, 考える必要があります。なぜなら, その状況によって, 日記をつける確率が変わるからです。
$n$ 日目に日記をつけた確率は $p_n$ なので, $n$ 日目に日記をつけなかった確率は $(1-p_n)$ となります。したがって, この2つの状況をふまえて, $(n+1)$ 日目に日記をつける状況を樹形図のように書くと以下のようになります。

したがって, $p_{n+1}$ は
$p_{n+1}=\dfrac23 p_n+\dfrac56(1-p_n)$
計算して
$p_{n+1}=-\dfrac16 p_n+\dfrac56\cdots$ (答)
(2) (1)より, 特性方程式 $x=-\dfrac16 x+\dfrac56$ を解くと,
$x=\dfrac57$
これより,
$p_{n+1}-\dfrac57=-\dfrac16\left(p_n-\dfrac57\right)$
$p_1=1$ なので,
数列 $\left(p_n-\dfrac57\right)$ は, 初項 $p_1-\dfrac57=\dfrac27$ , 公比 $-\dfrac16$ の等比数列になる。
したがって,
$p_n-\dfrac57\right=\dfrac27\left(-\dfrac16\right)^{n-1}$
よって,
$p_n=\dfrac57+\dfrac27\left(-\dfrac16\right)^{n-1}\cdots$ (答)
※(2)の答案で特性方程式のくだりは便宜上書いてありますが, 実際の解答用紙には書かない方がよいです。単に(1)より式変形すると～でいいです。

確率と漸化式

確率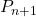 $P_{n+1}$ を考えるときは確率 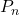$P_n$ の状況を考えられるだけ考えて関係式をつくること。その場合, 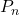$P_n$ (事象が起こる場合), 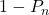$1-P_n$ (事象が起こらない場合)で考えれば大丈夫です。そこから, 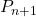$P_{n+1}$ との関係式をつくります。あとは, その漸化式を解けば, 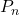$P_n$ は求まります。

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル