中学数学：2021年(令和3年)茨木県・高校入試　数学　展開図と立体

こんにちは。それでは早速問題です。プリントアウト用はこちら

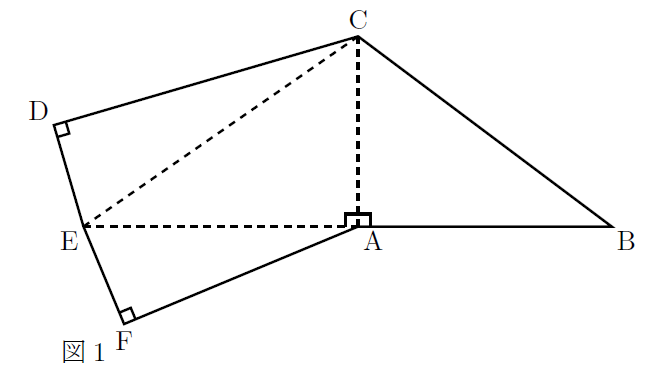
下の図1は, 三角すいの展開図であり, AB $=$ 12cm, AC $=$ 9cm, ED $=$ 5cmである。

(太郎さんと花子さんの会話)

太郎：辺ABと辺ACの長さがわかっているから, 三角形ABCの面積は簡単に求めることができるよ。他の
三角形の面積も求めることができるかな。

花子：辺EDの長さが5cmだから, 三角形CDEの面積もわかりそうね。
太郎：確かにそうだね。三角形CDEの面積は【ア】 $^2$ になるよ。
花子：次は, この展開図を組み立てて体積について考えてみましょう。
太郎：どの面を底面としてみると体積が求めやすいかな。
花子：組み立てたときに頂点が重なるところがあるので, 図2のように展開図に面, 面,面, 面と名前をつけて考えてみると, 面を三角すいの底面とするといいかもしれないね。

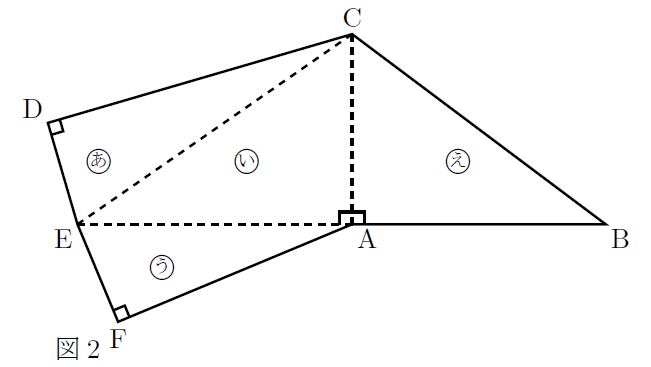
太郎：なるほど。そうすると, 面えと垂直になるのは【イ】だよ。
花子：これで体積を求めることができそうね。
太郎：計算してみたら, 三角すいの体積は【ウ】cm $^3$ になるよ。
花子：ところで, 底面とする面を変えてみると, 三角すいの高さが変わるわね。
太郎：なるほど。そうすると, 三角すいの高さが, 一番高くなるのは【エ】を底面にとしたときで, 一番低くなるのは【オ】を底面としたときだよ。
( 1 ) 会話中の【ア】に当てはまる数を求めなさい。
( 2 ) 会話中の【イ】に当てはまる面を, 面～面の中からすべて選んで, その記号を書きなさい。また, 【ウ】に当てはまる数を求めなさい。
( 3 ) 会話中の【エ】, 【オ】に当てはまる面を, 面～面の中から一つ選んで, その記号をそれぞれ書きなさい。
(2021茨木県)

答え

(1) 各辺の長さは次のようになります。CB, CE, AEは三平方の定理で求めています。

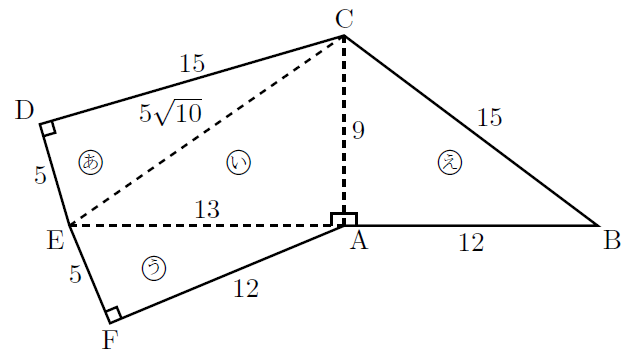
したがって, 面CDEの面積は,
$\dfrac12\times5\times15=\dfrac{75}{2}$
$\dfrac{75}{2}$ cm $^2$
【ア】＝ $\dfrac{75}{2}$
(2) 組み立てると以下のような形になります。図は底面を(え)としています。

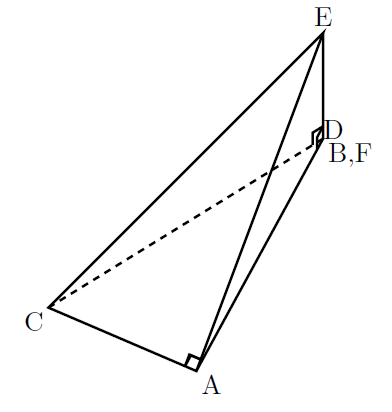
このとき, 底面(え)と垂直になるのは△CDE(面(あ))と△AEF(面(う))になります。
【イ】＝面(あ), 面(う)
体積は底面積が $\dfrac12\times9\times12=54$ , 高さがED $=$ 5なので,
求める体積は $\dfrac13\times54\times5=90$
90cm $^3$
【ウ】＝90
(3) 高さが一番高いということは底面積が一番小さいということなので, 面積が一番小さいのは, 面(う), 高さが一番低いということは底面積が一番大きいということなので, 面積が一番大きいのは面(い)。
したがって, 【エ】＝面(う), 【オ】＝面(い)

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル